
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
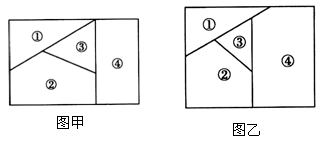
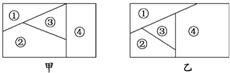 9、用n种不同的颜色为下列两块广告牌着色(如图甲、乙),要求在①②③④四个区域中相邻(有公共边界)的区域不用同一颜色.
9、用n种不同的颜色为下列两块广告牌着色(如图甲、乙),要求在①②③④四个区域中相邻(有公共边界)的区域不用同一颜色.查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
用n种不同颜色为下列两块广告牌着色(如下图甲、乙),要求在①、②、③、④个区域中相邻(有公共边的)区域不用同一种颜色.
(1)若n…=6,为甲着色时共有多种不同的方法?
(2)若为乙着色时共有120种不同的方法,求n.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
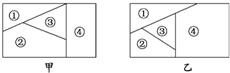 用n种不同的颜色为下列两块广告牌着色(如图甲、乙),要求在①②③④四个区域中相邻(有公共边界)的区域不用同一颜色.
用n种不同的颜色为下列两块广告牌着色(如图甲、乙),要求在①②③④四个区域中相邻(有公共边界)的区域不用同一颜色.查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:11.1 分类加法计数原理与分步乘法计数原理1(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com