
分析 (Ⅰ)当a=1时,f(x)=(x-5)cosx-sinx,从而化简可得x-5=tanx,作函数y=x-5与函数y=tanx在[0,π]上的图象,从而确定零点的个数;
(Ⅱ)求导f′(x)=-(ax-5)sinx,分类讨论以确定函数的单调性,从而求函数的最值,从而求|f(x1)-f(x2)|的最大值g(a)即可.
解答 解:(Ⅰ)当a=1时,f(x)=(x-5)cosx-sinx,
令(x-5)cosx-sinx=0得x-5=tanx,
作函数y=x-5与函数y=tanx在[0,π]上的图象如下,
故f(x)在[0,π]上有且只有一个零点;
(Ⅱ)∵f(x)=(ax-5)cosx-asinx,
∴f′(x)=acosx-(ax-5)sinx-acosx
=-(ax-5)sinx,
当πa-5≤0,即a≤$\frac{5}{π}$时,f′(x)>0在(0,π)上恒成立;
故f(x)=(ax-5)cosx-asinx在[0,π]上是增函数,
而fmin(x)=f(0)=-5cos0=-5,fmax(x)=f(π)=(aπ-5)cosπ-asinπ=5-aπ,
故g(a)=5-aπ-(-5)=10-aπ.
当a>$\frac{5}{π}$时,由导数知f(x)=(ax-5)cosx-asinx在[0,$\frac{5}{a}$)上是增函数,在($\frac{5}{a}$,π]上是减函数,
故fmax(x)=f($\frac{5}{a}$)=-asin$\frac{5}{a}$,
f(0)=-5,f(π)=5-aπ,
当$\frac{5}{π}$<a≤$\frac{10}{π}$时,f(π)-f(0)=10-aπ≥0,
故fmin(x)=f(0)=-5,
故g(a)=-asin$\frac{5}{a}$-(-5)=5-asin$\frac{5}{a}$;
当a>$\frac{10}{π}$时,
fmin(x)=f(π)=5-aπ,
故g(a)=-asin$\frac{5}{a}$-(5-aπ)=aπ-5-asin$\frac{5}{a}$;
综上所述,
g(a)=$\left\{\begin{array}{l}{10-aπ,a≤\frac{5}{π}}\\{5-asin\frac{5}{a},\frac{5}{π}<a≤\frac{10}{π}}\\{aπ-5-asin\frac{5}{a},a>\frac{10}{π}}\end{array}\right.$.
点评 本题考查了数形结合的思想及分类讨论的思想,同时考查了导数的综合应用,属于难题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | a2 | B. | $\frac{1}{2}{a^2}$ | C. | $\frac{1}{4}{a^2}$ | D. | $\frac{{\sqrt{3}}}{4}{a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{12}{13},5)$ | B. | $(-\frac{12}{13},-\frac{5}{13})$ | ||
| C. | $(\frac{12}{13},\frac{5}{13})$或$(-\frac{12}{13},-\frac{5}{13})$ | D. | $(±\frac{12}{13},±\frac{5}{13})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
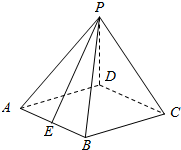 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,平面PED⊥平面PAB,PD⊥AD,点E为AB中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,平面PED⊥平面PAB,PD⊥AD,点E为AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)求证:BC⊥SB;
(1)求证:BC⊥SB;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com