练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设数列满足：，．

    （Ⅰ）求的通项公式及前项和；

    （Ⅱ）若等差数列满足， ，问：与的第几项相等？

    【答案】（I），（II）与数列的第项相等

    【解析】

    （Ⅰ）推导出数列{an}满足：a1＝1，an+1＝﹣2an，从而{an}是首项为1，公比为﹣2的等比数列，由此能求出{an}的通项公式和前n项和；（Ⅱ）由 b1＝﹣8，b2＝﹣6，{bn}为等差数列，求出{bn}的通项公式，从而b37＝2×37﹣10＝64．由此能求出b37与数列{an}的第7项相等．

    （Ⅰ）依题意，数列满足：，，

    所以是首项为1，公比为的等比数列.

    则的通项公式为，

    由等比数列求和公式得到：前项和.

    （Ⅱ）由 (Ⅰ) 可知，， ，

    因为为等差数列， .

    所以的通项公式为.

    所以.

    令，解得.

    所以与数列的第项相等.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若，求的单调区间；

    （2）若函数存在唯一的零点，且，则的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若存在正数，使恒成立，求实数的最大值；

    （2）设，若没有零点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    以平面直角坐标系xOy的原点为极点，x轴的正半轴为极轴，取相同的长度单位建立极坐标系，直线l的坐标方程为，曲线C的参数方程为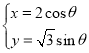（θ为参数）．

    （1）求直线l的直角坐标方程和曲线C的普通方程；

    （2）以曲线C上的动点M为圆心、r为半径的圆恰与直线l相切，求r的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， ， .

    （1）若是的充分不必要条件，求实数的取值范围；

    （2）若，“”为真命题，“”为假命题，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂的机器上存在一种易损元件，这种元件发生损坏时，需要及时维修. 现有甲、乙两名工人同时从事这项工作，下表记录了某月1日到10日甲、乙两名工人分别维修这种元件的件数.

    日期

    1日

    2日

    3日

    4日

    5日

    6日

    7日

    8日

    9日

    10日

    甲维修的元件数

    3

    5

    4

    6

    4

    6

    3

    7

    8

    4

    乙维修的元件数

    4

    7

    4

    5

    5

    4

    5

    5

    4

    7

    （1）从这天中，随机选取一天，求甲维修的元件数不少于5件的概率；

    （2）试比较这10天中甲维修的元件数的方差与乙维修的元件数的方差的大小.（只需写出结论）；

    （3）由于甲、乙的任务量大，拟增加工人，为使增加工人后平均每人每天维修的元件不超过3件，请利用上表数据估计最少需要增加几名工人.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

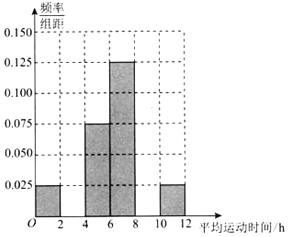
    【题目】已知某企业有职工5000人，其中男职工3500人，女职工1500人．该企业为了丰富职工的业余生活，决定新建职工活动中心，为此，该企业工会采用分层抽样的方法，随机抽取了300名职工每周的平均运动时间（单位：h），汇总得到频率分布表（如表所示），并据此来估计该企业职工每周的运动时间：

    平均运动时间

    频数

    频率

    [0，2）

    15

    0.05

    [2，4）

    m

    0.2

    [4，6）

    45

    0.15

    [6，8）

    755

    0.25

    [8，10）

    90

    0.3

    [10，12）

    p

    n

    合计

    300

    1

    （1）求抽取的女职工的人数；

    （2）①根据频率分布表，求出m、n、p的值，完成如图所示的频率分布直方图，并估计该企业职工每周的平均运动时间不低于4h的概率；

    男职工

    女职工

    总计

    平均运动时间低于4h

    平均运动时间不低于4h

    总计

    ②若在样本数据中，有60名女职工每周的平均运动时间不低于4h，请完成以下2×2列联表，并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”．

    附：K2=，其中n=a+b+c+d．

    P（K2≥k0）

    0.25

    0.15

    0.10

    0.05

    0.025

    k0

    1.323

    2.072

    2.706

    3.841

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的内角A，B，C的对边分别为a，b，c，若a=bcosC+csinB．

    （1）求B；

    （2）求y=sinA-sinC的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十八大以来，我国新能源产业迅速发展.以下是近几年某新能源产品的年销售量数据：

    年份

    2014

    2015

    2016

    2017

    2018

    年份代码

    1

    2

    3

    4

    5

    新能源产品年销售（万个）

    1.6

    6.2

    17.7

    33.1

    55.6

    （1）请画出上表中年份代码与年销量的数据对应的散点图，并根据散点图判断.

    与中哪一个更适宜作为年销售量关于年份代码的回归方程类型；

    （2）根据（Ⅰ）的判断结果及表中数据，建立关于的回归方程，并预测2019年某新能源产品的销售量（精确到0.01）.

    参考公式：，.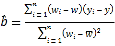

    参考数据：，，，，，，，其中.

    查看答案和解析>>

    同步练习册答案