
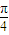 (k∈Z)”是“函数f(x)=sinx•cosx在x处取得最大值”的( )
(k∈Z)”是“函数f(x)=sinx•cosx在x处取得最大值”的( )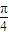 (k∈Z)时,得到函数f(x0 )=
(k∈Z)时,得到函数f(x0 )= ,是最大值,故充分性成立.当函数f(x)在x处取得最大值时,解得x0 =kπ+
,是最大值,故充分性成立.当函数f(x)在x处取得最大值时,解得x0 =kπ+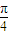 ,k∈z.故此时x不一定是2kπ+
,k∈z.故此时x不一定是2kπ+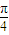 (k∈Z),故必要性不成立,由此得出结论.
(k∈Z),故必要性不成立,由此得出结论.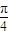 (k∈Z)时,函数f(x0 )=sinx•cosx=
(k∈Z)时,函数f(x0 )=sinx•cosx= sin2x0 =
sin2x0 = sin2(2kπ+
sin2(2kπ+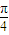 )=
)= ,
, sin2x 在x处取得最大值时,2 x0 =2kπ+
sin2x 在x处取得最大值时,2 x0 =2kπ+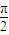 ,k∈z.
,k∈z.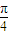 ,k∈z.故此时x不一定是2kπ+
,k∈z.故此时x不一定是2kπ+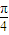 (k∈Z),故必要性不成立.
(k∈Z),故必要性不成立.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 1、已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有( )
1、已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有( )查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com