
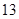 秒与
秒与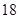 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组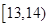 ,第二组
,第二组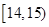 ,…,第五组
,…,第五组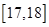 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.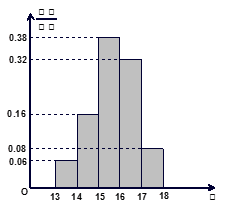
 .
.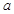 、
、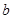 、
、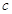 、
、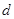 ,其中a为男生,b、c、d为女生,第一组三人记为1、2、3,其中1、2为男生,3为女生,基本事件列表如下:……… 7分
,其中a为男生,b、c、d为女生,第一组三人记为1、2、3,其中1、2为男生,3为女生,基本事件列表如下:……… 7分| | a | b | c | d |
| 1 | 1 a | 1b | 1c | 1d |
| 2 | 2 a | 2b | 2c | 2d |
| 3 | 3 a | 3b | 3c | 3d |
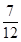 . …………………12分
. …………………12分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |

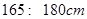 的概率;
的概率;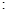 190cm之间的男生中任选2人,求至少有1人身高在185
190cm之间的男生中任选2人,求至少有1人身高在185 190cm之间的概率。
190cm之间的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
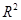 来刻画回归的效果时,
来刻画回归的效果时,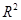 的值越小,说明模型拟合的效果越好;
的值越小,说明模型拟合的效果越好;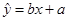 和各点
和各点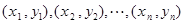 的偏差
的偏差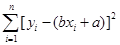 是该坐标平面上所有直线与这些点的偏差中最小的直线.
是该坐标平面上所有直线与这些点的偏差中最小的直线. | A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.10 | B.8 | C.7 | D.6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.55,67,19,98,10 | B.556,719,810,507,175 |
| C.785,567,199,507,175 | D.556,719,050,717,512 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 甲 | 60 | 80 | 70 | 90 | 70 |
| 乙 | 80 | 60 | 70 | 80 | 75 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| | 患慢性气管炎 | 未患慢性气管炎 | 合计 |
| 吸烟 | 20 | 20 | 40 |
| 不吸烟 | 5 | 55 | 60 |
| 合计 | 25 | 75 | 100 |
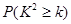 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
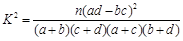
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com