
【题目】如图1所示,在边长为12的正方形AA'A1'A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1'分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A'A1'与AA1重合,构成如图2所示的三棱柱ABC﹣A1B1C1.
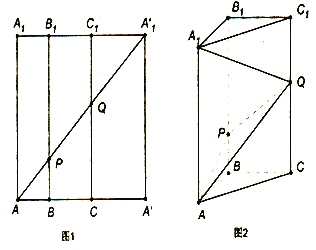
(1)求三棱锥P﹣ABC与三棱锥Q﹣PAC的体积之和;
(2)求直线AQ与平面BCC1B1所成角的正弦值;
(3)求三棱锥Q﹣ABC的外接球半径r.
【答案】(1)体积之和为20.(2)![]() .(3)
.(3)![]() .
.
【解析】试题分析:(1)在图1中,∵△PAB,△ACQ是等腰直角三角形,∴PB=3,CQ=7,∵AB=3,BC=4,AC=12﹣3﹣4=5,∴AB⊥BC,∴B到AC的距离d=![]() ,分别计算VP﹣ABC,VQ﹣PAC得出结论;(2)连接BQ,∵BB1⊥平面ABC,∴BB1⊥AB,又AB⊥BC,BC∩BB1=B,∴AB⊥平面BCC1B1,∴∠AQB是直线AQ与平面BCC1B1所成角;(3)取AQ中点M,∵△ABQ和△ACQ是直角三角形,∴MA=MB=MC=MQ,∴三棱锥Q﹣ABC的外接球球心为M,从而得出外接球半径.
,分别计算VP﹣ABC,VQ﹣PAC得出结论;(2)连接BQ,∵BB1⊥平面ABC,∴BB1⊥AB,又AB⊥BC,BC∩BB1=B,∴AB⊥平面BCC1B1,∴∠AQB是直线AQ与平面BCC1B1所成角;(3)取AQ中点M,∵△ABQ和△ACQ是直角三角形,∴MA=MB=MC=MQ,∴三棱锥Q﹣ABC的外接球球心为M,从而得出外接球半径.
试题解析:
(1)在图1中,∵△PAB,△ACQ是等腰直角三角形,
∴PB=3,CQ=7,
∵AB=3,BC=4,AC=12﹣3﹣4=5,
∴AB⊥BC,
∴B到AC的距离d=![]() =
=![]() .
.
∴VP﹣ABC=![]() =
=![]() =6,
=6,
VQ﹣PAC=VP﹣QAC=![]() =
=![]() =14,
=14,
∴三棱锥P﹣ABC与三棱锥Q﹣PAC的体积之和为6+14=20.
(2)连接BQ,
∵BB1⊥平面ABC,∴BB1⊥AB,
又AB⊥BC,BC∩BB1=B,
∴AB⊥平面BCC1B1,
∴∠AQB是直线AQ与平面BCC1B1所成角.
∵AQ=![]() =
=![]() ,
,
∴sin∠AQB=![]() =
=![]() .
.
(3)设AQ的中点为M,
∵△ABQ和△ACQ是直角三角形,
∴MA=MB=MC=MQ,
∴三棱锥Q﹣ABC的外接球球心为M.
∴三棱锥Q﹣ABC的外接球半径r=![]() AQ=
AQ=![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】对于区间![]() ,若函数
,若函数![]() 同时满足:①
同时满足:①![]() 在
在![]() 上是单调函数;②函数
上是单调函数;②函数![]() ,
,![]() 的值域是
的值域是![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的“保值”区间.
的“保值”区间.
(1)求函数![]() 的所有“保值”区间.
的所有“保值”区间.
(2)函数![]() 是否存在“保值”区间?若存在,求出
是否存在“保值”区间?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中, ![]() 底面
底面![]() 分别是
分别是![]() 的中点,
的中点, ![]() 在
在![]() ,且
,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;
的长;
若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某奶茶公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的奶茶共5 杯,其颜色完全相同,并且其中3杯为![]() 奶茶,另外2杯为
奶茶,另外2杯为![]() 奶茶,公司要求此员工一一品尝后,从5杯奶茶中选出2杯奶茶.若该员工2杯都选
奶茶,公司要求此员工一一品尝后,从5杯奶茶中选出2杯奶茶.若该员工2杯都选![]() 奶茶,则评为优秀;若2 杯选对1杯
奶茶,则评为优秀;若2 杯选对1杯![]() 奶茶,则评为良好;否则评为及格.假设此人对
奶茶,则评为良好;否则评为及格.假设此人对![]() 和
和![]() 两种奶茶没有鉴别能力.
两种奶茶没有鉴别能力.
(Ⅰ)求此人被评为优秀的概率;(Ⅱ)求此人被评为良好及以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
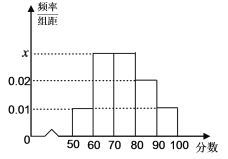
【题目】2018年高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试,现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
,![]() ,…,
,…,![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(Ⅰ)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
(Ⅱ)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取2人参加这次考试的考后分析会,试求![]() 组中至少有1人被抽到的概率.
组中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
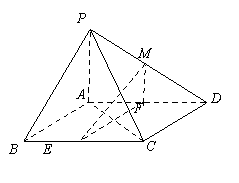
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com