分析:(1)分别画出分段函数的图象,如图所示,由图象可得出单调递增及递减区间;
(2)当x=-3时,f(x)=x+2,确定出f(-3)的值为-1,而-1大于-2小于1,得到此时f(x)=x2+2x,将x=-1代入即可求出所求式子的值;
(3)由f(a)=3,根据函数图象得到2a-1=3,即可求出a的值;
(4)分三种情况考虑:当m小于等于-2时,m大于-2小于1时,m大于等于1时,分别由确定出f(m),代入所求不等式中,求出m的范围即可.
解答: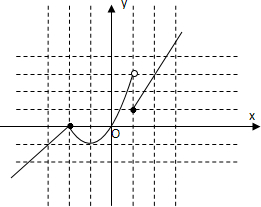
解:(1)图象如右,
它的单调增区间是(-∞,-2],[-1,1),[1,+∞);
它的单调减区间是(-2,-1);
(2)∵-3<-2,∴f(-3)=-3+2=-1;
∵-2<-1<1,∴f(f(-3))=f(-1)=(-1)
2+2×(-1)=-1;
(3)∵f(a)=3,∴2a-1=3,
解得:a=2;
(4)当m≤-2时,f(m)=m+2>m恒成立;
当-2<m<1时,f(x)=m
2+2m>m,
解得:m>0或m<-1,
此时m的范围为:-2<m<-1或0<m<1;
当m≥1时,f(m)=2m-1>m,
解得:m>1,
综上,实数m的取值范围为:m<-1或0<m<1或m>1.
点评:此题考查了一元二次不等式的解法,利用了数形结合及分类讨论的思想,是一道高考中常考的基本题型.

 已知f(x)=
已知f(x)= 解:(1)图象如右,
解:(1)图象如右,

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案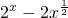 ,又a是函数g (x)=
,又a是函数g (x)=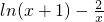 的正零点,则f(-2),f(a),f(1.5)的大上关系是
的正零点,则f(-2),f(a),f(1.5)的大上关系是