
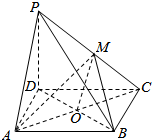
 如图,已知P为平行四边形ABCD所在平面外一点,M是线段PC的中点.
如图,已知P为平行四边形ABCD所在平面外一点,M是线段PC的中点.分析 (1)用$\overrightarrow{MB},\overrightarrow{MD}$表示出$\overrightarrow{PA}$即可;
(2)证明M,A,B,C不共面;
(3)用$\overrightarrow{MA},\overrightarrow{MB},\overrightarrow{MC}$表示出$\overrightarrow{PD}$,求出x,y,z.
解答 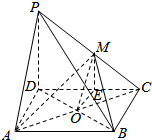 解:(1)∵四边形ABCD是平行四边形,∴O是BD中点,
解:(1)∵四边形ABCD是平行四边形,∴O是BD中点,
∴$\overrightarrow{MO}$=$\frac{1}{2}$($\overrightarrow{MB}+\overrightarrow{MD}$)=$\frac{1}{2}$$\overrightarrow{MB}$+$\frac{1}{2}$$\overrightarrow{MD}$,
∵M是线段PC的中点,∴$\overrightarrow{PA}$=2$\overrightarrow{MO}$=$\overrightarrow{MB}+\overrightarrow{MD}$,
∴向量$\overrightarrow{PA}$,$\overrightarrow{MB}$,$\overrightarrow{MD}$共面.
(2)∵M,A,B,C不在同一平面内,∴向量$\overrightarrow{MA}$,$\overrightarrow{MB}$,$\overrightarrow{MC}$不共面.
(3)取CD中点E,连结ME,OE,则$\overrightarrow{PD}$=2$\overrightarrow{ME}$=2($\overrightarrow{MO}+\overrightarrow{OE}$)=2$\overrightarrow{MO}$+2$\overrightarrow{OE}$=2$\overrightarrow{MO}$+$\overrightarrow{BC}$
=$\overrightarrow{MA}+\overrightarrow{MC}$+($\overrightarrow{MC}-\overrightarrow{MB}$)=$\overrightarrow{MA}-\overrightarrow{MB}+2\overrightarrow{MC}$.
∴x=1,y=-1,z=2,∴x+y+z=2.
点评 本题考查了平面向量的基本定理及其意义,用向量表示其他向量是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
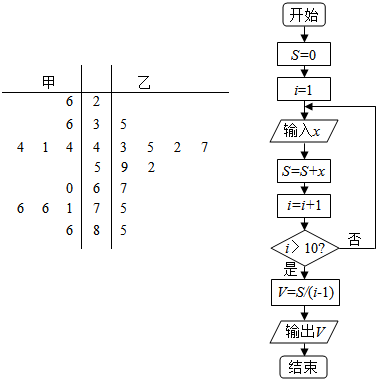 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com