
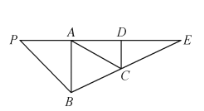
【题目】如图,在![]() 中,
中,![]() ,D是AE的中点,C是线段BE上的一点,且
,D是AE的中点,C是线段BE上的一点,且![]() ,
,![]() ,将
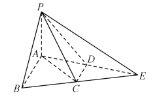
,将![]() 沿AB折起使得二面角
沿AB折起使得二面角![]() 是直二面角.
是直二面角.
(l)求证:CD平面PAB;
(2)求直线PE与平面PCD所成角的正切值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,
时,![]() ,
,![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设曲线![]() ,点
,点![]() ,
,![]() 为该曲线上不同的两点.求证:当
为该曲线上不同的两点.求证:当![]() 时,直线
时,直线![]() 的斜率大于-1.
的斜率大于-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=-![]() .
.
(1)求证:f(x)是R上的单调减函数.
(2)求f(x)在[-3,3]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() )+sin(2x﹣
)+sin(2x﹣ ![]() )+2cos2x﹣1,x∈R.
)+2cos2x﹣1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的方程是
的方程是![]() (
(![]() ,
,![]() ).
).
(1)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 围成的区域的面积;
围成的区域的面积;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() 轴上方的两点
轴上方的两点![]() ,
,![]() ,且
,且![]() ,求点
,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com