
【题目】已知a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(1)求函数f(x)的极值;
(2)求证:当a>ln2﹣1且x>0时,ex>2x﹣2a.
【答案】
(1)解:∵f(x)=ex﹣2x+2a,x∈R,
∴f′(x)=ex﹣2,x∈R.令f′(x)=0,得x=ln2.
于是当x变化时,f′(x),f(x)的变化情况如下表:
x | (﹣∞,ln2) | ln2 | (ln2,+∞) |
f′(x) | ﹣ | 0 | + |
f(x) | 单调递减 | 2(1﹣ln2+a) | 单调递增 |
故f(x)的单调递减区间是(﹣∞,ln2),单调递增区间是(ln2,+∞),
f(x)在x=ln2处取得极小值,极小值为f(ln2)=eln2﹣2ln2+2a=2(1﹣ln2+a)
(2)证明:设g(x)=ex﹣2x+2a,x>0,
于是g′(x)=ex﹣2,x>0.
由(1)知,当x∈(0,ln2)时,g′(x)<0,当x∈(ln2,+∞)时,g′(x)>0,
g(x)最小值为g(ln2)=eln2﹣2ln2+2a=2(a﹣ln2+1).
于是当a>ln2﹣1时,对任意x∈(0,+∞),都有g(x)>g(ln2)>0.
从而,当a>ln2﹣1且x>0时,ex>2x﹣2a
【解析】(1)由f(x)=ex﹣2x+2a,x∈R,知f′(x)=ex﹣2,x∈R.令f′(x)=0,得x=ln2.列表讨论能求出f(x)的单调区间及极值;(2)设g(x)=ex﹣2x+2a,x>0,于是g′(x)=ex﹣2.由(1)知当a>ln2﹣1时,g(x)最小值为g(ln2)=2(1﹣ln2+a).于是当a>ln2﹣1且x>0时,都有g(x)>0,即ex>2x﹣2a.
【考点精析】通过灵活运用函数的极值与导数和函数的最大(小)值与导数,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() 满足|
满足| ![]() |=|
|=| ![]() =1,且|k
=1,且|k ![]() +
+ ![]() |=
|= ![]() |
| ![]() ﹣k
﹣k ![]() |(k>0),令f(k)=
|(k>0),令f(k)= ![]()
![]() . (Ⅰ)求f(k)=
. (Ⅰ)求f(k)= ![]()
![]() (用k表示);
(用k表示);
(Ⅱ)若f(k)≥x2﹣2tx﹣ ![]() 对任意k>0,任意t∈[﹣1,1]恒成立,求实数x的取值范围.
对任意k>0,任意t∈[﹣1,1]恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,a2=3,an>0,且满足an+12﹣an=an+1+an2(n∈N*).
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)设 ![]() (λ为正偶数,n∈N*),是否存在确定λ的值,使得对任意n∈N* , 有Cn+1>Cn恒成立,若存在,求出λ的值,若不存在,说明理由.
(λ为正偶数,n∈N*),是否存在确定λ的值,使得对任意n∈N* , 有Cn+1>Cn恒成立,若存在,求出λ的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,则( )
A.f(x)在(0,+∞)上是增函数
B.f(x)在 ![]() 上是增函数
上是增函数
C.当x∈(0,1)时,f(x)有最小值 ![]()
D.f(x)在定义域内无极值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m 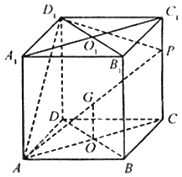
(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为 ![]() ;
;
(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中 ①若loga3>logb3,则a>b;
②函数f(x)=x2﹣2x+3,x∈[0,+∞)的值域为[2,+∞);
③设g(x)是定义在区间[a,b]上的连续函数.若g(a)=g(b)>0,则函数g(x)无零点;
④函数 ![]() 既是奇函数又是减函数.
既是奇函数又是减函数.
其中正确的命题有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=﹣ ![]() x2+bln(x+2)在区间[﹣1,2]不单调,则b的取值范围是( )
x2+bln(x+2)在区间[﹣1,2]不单调,则b的取值范围是( )
A.(﹣∞,﹣1]
B.[8,+∞)
C.(﹣∞,﹣1]∪[8,+∞)
D.(﹣1,8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com