
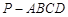 的底面
的底面 为菱形,
为菱形,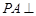 平面
平面 ,
,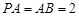 , E、F分别为
, E、F分别为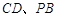 的中点,
的中点,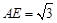 .
.
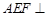 平面
平面 .
. 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.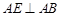 .
. 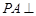
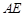 .由
.由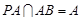 ,证出
,证出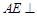 平面
平面 ,所以,平面
,所以,平面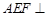 平面
平面 .
.  与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为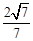 .
.  是菱形,
是菱形,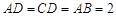 .
.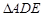 中,
中,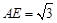 ,
,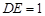 ,
,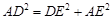 .
.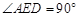 ,即
,即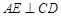 .
.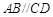 , ∴
, ∴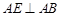 .…………………2分
.…………………2分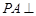 平面
平面 ,
,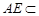 平面
平面 ,
,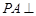
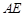 .又∵
.又∵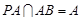 ,
,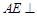 平面
平面 ,………………………………………4分
,………………………………………4分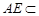 平面
平面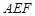 ,
,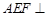 平面
平面 . ………………………………6分
. ………………………………6分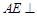 平面
平面 ,而
,而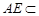 平面
平面 ,
,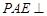 平面
平面 ………………………7分
………………………7分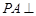 平面
平面 ,∴
,∴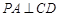 .
.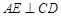 ,又
,又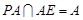
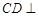 平面
平面 ,又
,又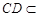 平面
平面 ,
, 平面
平面 .…………………………9分
.…………………………9分 是平面
是平面 与平面
与平面 的公垂面.
的公垂面.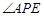 就是平面
就是平面 与平面
与平面 所成的锐二面角的平面角.……10分
所成的锐二面角的平面角.……10分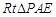 中,
中,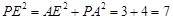 ,即
,即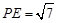 .……………11分
.……………11分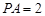 ,
,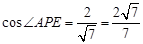 .
. 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为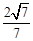 .…………14分
.…………14分
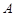 为原点,
为原点,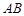 、
、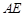 分别为
分别为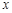 轴、
轴、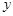 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系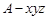 ,如图所示.因为
,如图所示.因为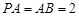 ,
,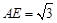 ,所以,
,所以,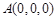 、
、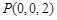 、
、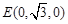 、
、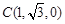 ,…………7分
,…………7分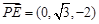 ,
,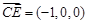 ,
,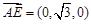 .………8分
.………8分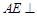 平面
平面 ,
, 的一个法向量为
的一个法向量为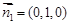 .……………………9分
.……………………9分 的一个法向量为
的一个法向量为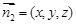 ,
,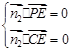 ,即
,即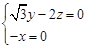 ,令
,令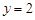 ,
,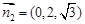 . …………………11分
. …………………11分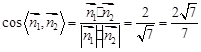 .
. 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为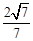 .……14分
.……14分

科目:高中数学 来源:不详 题型:单选题
 是
是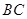 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持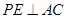 .则动点
.则动点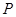 的轨迹与△
的轨迹与△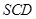 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )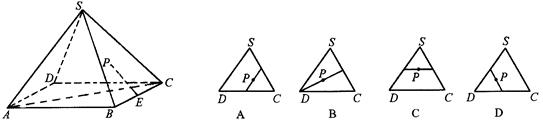
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,底面
中,底面 是正方形,侧面
是正方形,侧面 是正三角形,且平面
是正三角形,且平面 ⊥底面
⊥底面

 ⊥平面
⊥平面
 与底面
与底面 所成角的余弦值;
所成角的余弦值; ,求点
,求点 到平面
到平面 的距离.
的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com