
(1)若平面PAB∩平面PCD=l,试判断直线l与平面ABCD的关系,并加以证明;
(2)求平面PAB与平面PCD所成二面角的大小;
(3)当AD为多长时,点D到平面PCE的距离为2?
(文)在正四棱柱ABCD—A1B1C1D1中,BB1=2AB=4,E、F分别是棱AB与BC的中点.
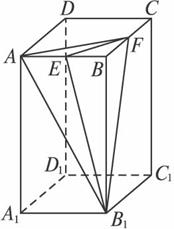
(1)求二面角EFB1B的平面角的正切值.
(2)在棱DD1上能否找到一点M,使BM⊥平面B1EF?若能,试确定M的位置;若不能,请说明理由.
解:(理)(1)l与面ABCD平行.证明:∵DC∥AB,DC![]() 面PAB,∴DC∥面PAB.∵DC
面PAB,∴DC∥面PAB.∵DC![]() 面PDC,面PAB∩面PCD=l,∴l∥DC.又l
面PDC,面PAB∩面PCD=l,∴l∥DC.又l![]() 面ABCD,DC
面ABCD,DC![]() 面ABCD,∴l∥面ABCD.
面ABCD,∴l∥面ABCD.
(2)由(1),可知面PAB∩面PCD=l.∵面PAD⊥面ABCD,ABCD为矩形,∴AB⊥面PAD.∵l∥DC∥AB,∴l⊥面PAD.∴l⊥AD.同理,l⊥AP.∴∠PAD为面PAB与面PDC所成二面角的平面角.∵△PAD是正三角形,∴面PAB与面PDC所成二面角大小为60°.
(3)设AD的中点为F,且AD=a,则PF⊥AD.∴∠PCF=30°.∴PF=![]() a.∴CF=
a.∴CF=![]() a,CD=
a,CD=![]() a.
a.
由VD—PEC=VP—DEC,得![]() S△DEC·PF=
S△DEC·PF=![]() S△PEC·2.∴
S△PEC·2.∴![]() ·a·
·a·![]() a·
a·![]() =2·S△PEC,①
=2·S△PEC,①
易求PE=EC=![]() a,PC=
a,PC=![]() a.∴S△PCE=
a.∴S△PCE=![]() |PC|
|PC|![]() .②
.②
由①②,得a=![]() .
.
(文)(1)过B点作BG⊥B1F,垂足为G点,连结EG.∵EB⊥面BB1C1C,根据三垂线定理,知∠EGB即为所求二面角的平面角.
EB=![]() AB=1,BG=
AB=1,BG=![]() .∴tan∠EGB=
.∴tan∠EGB=![]() ,二面角EFB1B的平面角的正切值为
,二面角EFB1B的平面角的正切值为![]() .
.
(2)设存在M点.

EF∩DB=H.已知BD=![]() ,BH=
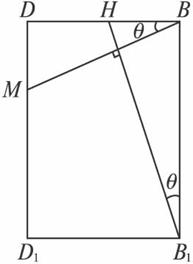
,BH=![]() .∵EF⊥面BB1D1D,∴EF⊥B1H,EF⊥BM.在如图所示的截面中,BM⊥B1H,
.∵EF⊥面BB1D1D,∴EF⊥B1H,EF⊥BM.在如图所示的截面中,BM⊥B1H,
∴tanθ=![]() .∴DM=
.∴DM=![]() ,即存在点M,且D1M=
,即存在点M,且D1M=![]() 或DM=
或DM=![]() .
.


科目:高中数学 来源: 题型:
(09年临沭县模块考试理)(12分)
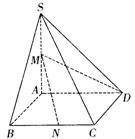
如图,在四棱锥S―ABCD中,底面ABCD是边长为1的菱形,∠ABC=![]() ,SA⊥底面
,SA⊥底面
ABCD,SA=2,M 的为SA的中点,N在线段BC上。
(Ⅰ)当![]() 为何值时,MN∥平面SCD;(说明理由)。
为何值时,MN∥平面SCD;(说明理由)。
(Ⅱ)求MD和平面SCD所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年西工大附中理)如图,在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 平面
平面![]() ,
,![]() 与底面成
与底面成![]() 角.
角.
(Ⅰ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅱ) 求二面角![]() 的大小;
的大小;
(Ⅲ) 若![]() ,
,![]() 为垂足,求异面直线
为垂足,求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
(06年重庆卷理)(13分)
如图,在四棱锥![]() 中,
中,![]() 底面ABCD,
底面ABCD,![]() 为直角,
为直角,![]() ,
,![]() E、F分别为
E、F分别为![]() 、
、![]() 中点。
中点。
(I)试证:![]() 平面
平面![]() ;
;
(II)高![]() ,且二面角
,且二面角 ![]() 的平面角大小
的平面角大小![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
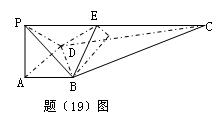
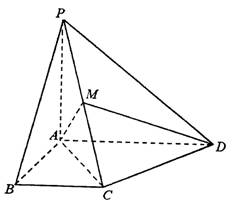
(08年重点中学模拟理) (12分)如图,在四棱锥P―ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD//BC且AD>BC,∠DAB=∠ABC=90°,PA=![]() ,AB=BC=1。M为PC的中点。
,AB=BC=1。M为PC的中点。
(1)求二面角M―AD―C的大小;
(2)如果∠AMD=90°,求线段AD的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
(04年天津卷理)(12分)
如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱![]() 底面ABCD,
底面ABCD,![]() ,E是PC的中点,作
,E是PC的中点,作![]() 交PB于点F。
交PB于点F。
(I)证明 ![]() 平面
平面![]() ;
;
(II)证明![]() 平面EFD;
平面EFD;
(III)求二面角![]() 的大小。
的大小。
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com