
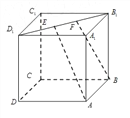
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的两个动点,且
上的两个动点,且![]() ,则下列结论错误的是 ( )
,则下列结论错误的是 ( )
A. ![]()
B. 直线![]() 、
、![]() 所成的角为定值
所成的角为定值
C. ![]() ∥平面
∥平面![]()
D. 三棱锥![]() 的体积为定值
的体积为定值
【答案】B
【解析】
在A中,∵正方体![]()
∴AC⊥BD,AC⊥![]() ,
,
∵BD∩![]() =B,∴AC⊥平面
=B,∴AC⊥平面![]() ,
,
∵BF平面![]() ,∴AC⊥BF,故A正确;
,∴AC⊥BF,故A正确;
在B中,异面直线AE、BF所成的角不为定值,因为当F与![]() 重合时,令上底面顶点为O,点E与O重合,则此时两异面直线所成的角是
重合时,令上底面顶点为O,点E与O重合,则此时两异面直线所成的角是![]() ;当E与
;当E与![]() 重合时,此时点F与O重合,则两异面直线所成的角是
重合时,此时点F与O重合,则两异面直线所成的角是![]() ,此二角不相等,故异面直线AE、BF所成的角不为定值.故B错误
,此二角不相等,故异面直线AE、BF所成的角不为定值.故B错误
在C中,∵EF∥BD,BD平面ABCD,EF平面ABCD,∴EF∥平面ABCD,故C正确;
在D中,∵AC⊥平面![]() ,∴A到平面BEF的距离不变,
,∴A到平面BEF的距离不变,
∵B到EF的距离为1,![]() ,∴△BEF的面积不变,
,∴△BEF的面积不变,
∴三棱锥A-BEF的体积为定值,故D正确;


科目:高中数学 来源: 题型:
【题目】蚌埠市某中学高三年级从甲(文)、乙(理)两个科组各选出![]() 名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是
名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是![]() ,乙组学生成绩的中位数是
,乙组学生成绩的中位数是![]() .
.
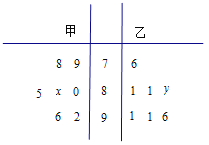
(1)求![]() 和
和![]() 的值;
的值;
(2)计算甲组![]() 位学生成绩的方差
位学生成绩的方差![]() ;
;
(3)从成绩在![]() 分以上的学生中随机抽取两名学生,求甲组至少有一名学生的概率.
分以上的学生中随机抽取两名学生,求甲组至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围;
(2)若函数y=f(x)在[m,n]上的值域是[m,n],求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的椭圆![]() 的两焦点分别为双曲线
的两焦点分别为双曲线![]() 的顶点,直线
的顶点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 外的点
外的点![]() 满足
满足![]() ,
, ![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)试确定点![]() 的坐标,使得
的坐标,使得![]() 的面积最大,并求出最大面积.
的面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(Ⅰ)求![]() 、
、![]() 的值;
的值;
(Ⅱ)设![]() .
.
(i)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(ii)若函数![]() 有三个不同的零点,求实数
有三个不同的零点,求实数![]() 的取值范围(
的取值范围(![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定于符号函数![]() ,已知
,已知![]() ,
,![]() ,
,
(1)求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的最小值;
的最小值;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 上有唯一零点,求
上有唯一零点,求![]() 的取值范围;
的取值范围;
(3)已知存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com