
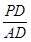 =
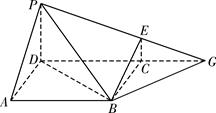
=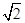 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.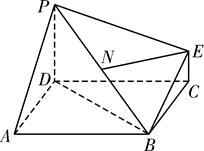
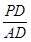 =
=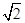 ,以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系
,以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系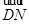 为平面PBE的法向量.
为平面PBE的法向量.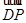 为平面ABCD的法向量,利用向量的夹角公式得到结论
为平面ABCD的法向量,利用向量的夹角公式得到结论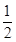 PD.
PD.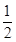 PD,(2分)
PD,(2分)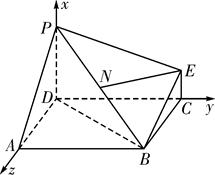
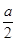 ),N(
),N(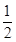 ,
,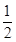 ,
,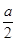 ),
),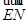 =(
=(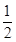 ,-
,-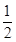 ,0),
,0),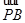 =(1,1,-a),
=(1,1,-a),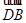 =(1,1,0).
=(1,1,0).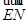 ·
·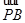 =
=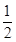 ×1-
×1-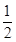 ×1-a×0=0,
×1-a×0=0,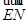 ·
·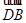 =
=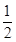 ×1-
×1-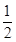 ×1+0×0=0,
×1+0×0=0,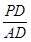 =
=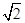 ,DB=
,DB=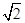 AD,∴PD=DB,∴DN⊥PB,∴
AD,∴PD=DB,∴DN⊥PB,∴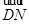 为平面PBE的法向量.
为平面PBE的法向量.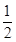 ,
,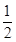 ,
,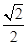 ),∴
),∴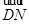 =(
=(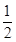 ,
,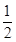 ,
,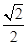 ).
).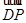 为平面ABCD的法向量,
为平面ABCD的法向量,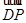 =(0,0,
=(0,0,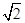 ),(10分)
),(10分)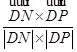 =
=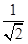 =
=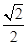 ,
,


科目:高中数学 来源:不详 题型:解答题
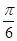 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD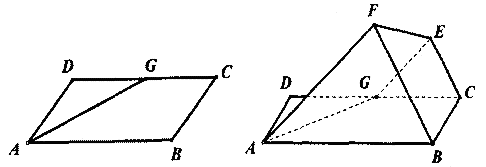
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
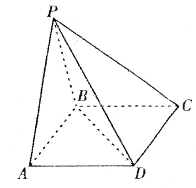
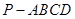 的底面
的底面 是矩形,
是矩形,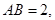
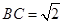 ,且侧面
,且侧面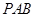 是正三角形,平面
是正三角形,平面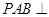 平面
平面 ,
,
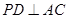 ;
; 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角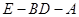 的大小为45°.若存在,试求
的大小为45°.若存在,试求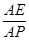 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
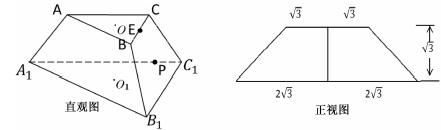
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 处,同一时刻,一个长
处,同一时刻,一个长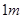 ,一端接触地面且与地面垂直的竹竿的影子长为
,一端接触地面且与地面垂直的竹竿的影子长为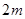 ,则该球的半径等于( )
,则该球的半径等于( )A.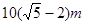 | B. | C.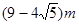 | D.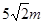 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
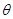 角的直线一定有无穷多条。
角的直线一定有无穷多条。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
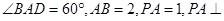 平面ABCD,E是PC的中点,F是AB的中点。
平面ABCD,E是PC的中点,F是AB的中点。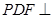 平面PAB;
平面PAB;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com