
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() .现将四边形
.现将四边形![]() 沿直线
沿直线![]() 翻折,使翻折后的二面角
翻折,使翻折后的二面角![]() 的余弦值为
的余弦值为![]() .
.
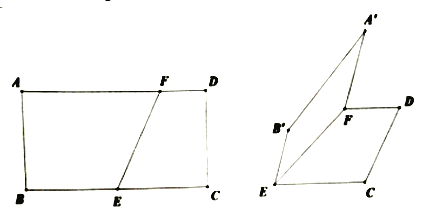
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为 ![]() 米,tanA=
米,tanA= ![]() ,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)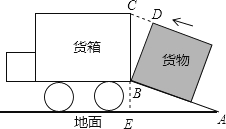
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令![]() 表示实施方案
表示实施方案![]() 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.
(Ⅰ)求![]() ,
, ![]() 的分布列;
的分布列;
(Ⅱ)不管实施哪种方案, ![]() 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称.
对称.
(1)求m,k的值;
(2)若直线![]() 与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y=﹣ ![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).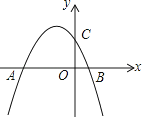
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线![]() 对称的圆的方程;
对称的圆的方程;
(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点![]() ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系xOy中,圆C的参数方程![]() 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆C的交点为O、P,与直线
与圆C的交点为O、P,与直线![]() 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com