
分析 (1)根据平面向量的数量积与夹角公式,即可求出两向量夹角的余弦值;
(2)根据平面向量的坐标运算与两向量垂直,数量积为0,列出方程求出λ的值.
解答 解:(1)向量$\overrightarrow{a}$=(-2,4),$\overrightarrow{b}$=(-1,-2),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=-2×(-1)+4×(-2)=-6,
|$\overrightarrow{a}$|=$\sqrt{{(-2)}^{2}{+4}^{2}}$=2$\sqrt{5}$,
|$\overrightarrow{b}$|=$\sqrt{{(-1)}^{2}{+(-2)}^{2}}$=$\sqrt{5}$;
∴$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值为
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{-6}{2\sqrt{5}×\sqrt{5}}$=-$\frac{3}{5}$;
(2)∵$\overrightarrow{a}$-λ$\overrightarrow{b}$=(-2,4)-(-λ,-2λ)=(λ-2,2λ+4),
2$\overrightarrow{a}$+$\overrightarrow{b}$=(-4,8)+(-1,-2)=(-5,6);
又向量$\overrightarrow{a}$-λ$\overrightarrow{b}$与2$\overrightarrow{a}$+$\overrightarrow{b}$垂直,
∴($\overrightarrow{a}$-2λ$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=-5(λ-2)+6(2λ+4)=0,
解得λ=-$\frac{34}{7}$.
点评 本题考查了平面向量的数量积运算与夹角公式的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 有两个内角是钝角 | B. | 有三个内角是钝角 | ||
| C. | 至少有两个内角是钝角 | D. | 没有一个内角是钝角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
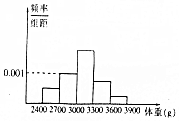
| A. | 0.001 | B. | 0.1 | C. | 0.2 | D. | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{3}$) | B. | (-$\frac{1}{3}$,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{3}$,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}{a^2}$ | B. | $\frac{{\sqrt{3}}}{4}{a^2}$ | C. | $\frac{{\sqrt{6}}}{2}{a^2}$ | D. | $\sqrt{6}{a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 价格 | 5000元及以上 | 3000元-4999元 | 1000元-2999元 | 1000元以下 |
| 45岁及以下 | 12 | 28 | 66 | 4 |
| 45岁以上 | 3 | 17 | 46 | 24 |
| P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com