
【题目】已知函数f(x)=![]() cos(2x-
cos(2x-![]() ),x∈R.
),x∈R.
(1)求函数f(x)单调递减区间;
(2)求函数f(x)在区间[-![]() ,
, ![]() ]上的最小值和最大值,并求出取得最值时x的值.
]上的最小值和最大值,并求出取得最值时x的值.
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数x≤3;②标准差s≤2;③平均数x≤3且标准差s≤2;④平均数x≤3且极差小于或等于2;⑤众数等于1且极差小于或等于4.
A. ①② B. ③④ C. ③④⑤ D. ④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生的数学测试成绩的频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20,则a的估计值是( )
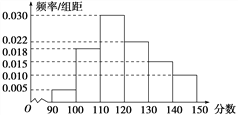
A. 130 B. 140 C. 133 D. 137
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足对任意
,如果满足对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]()
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界,已知函数
的上界,已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,判断函数
上的值域,判断函数![]() 在
在![]() 上是否为有界函数,并说明理由.
上是否为有界函数,并说明理由.
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=a(x﹣5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y=2x2和直线l:y=kx+1,O为坐标原点.
(1)求证:l与C必有两交点;
(2)设l与C交于A(x1 , y1)、B(x2 , y2)两点,且直线OA和OB的斜率之和为1,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在山顶![]() 点已测得
点已测得![]() ,
,![]() ,
,![]() 的俯角分别为
的俯角分别为![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() 为山脚两侧共线的三点,现欲沿直线
为山脚两侧共线的三点,现欲沿直线![]() 开通穿山隧道,为了求出隧道
开通穿山隧道,为了求出隧道![]() 的长,至少还需要直接测量出
的长,至少还需要直接测量出![]() ,
,![]() ,
,![]() 中的哪些线段长?把你上一问指出的需要测量得线段长和已测得的角度作为已知量,写出计算隧道
中的哪些线段长?把你上一问指出的需要测量得线段长和已测得的角度作为已知量,写出计算隧道![]() 的步骤.
的步骤.

解:
步骤![]() :还需要直接测量得线段为.
:还需要直接测量得线段为.
步骤![]() :计算线段.
:计算线段.
计算步骤:
步骤![]() :计算线段
:计算线段
计算步骤:
步骤![]() :计算线段
:计算线段
计算步骤:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加考试的机会,一量某次考试通过,便可领取驾照,不再参加以后的考试,否则就一直考到第4次为止如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9.求在一年内李明参加驾照考试次数ξ的分布列和ξ的期望,并求李明在一所内领到驾照的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一容量为50的样本,数据的分组以及各组的频数如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),5;[30.5,33.5],4.
(1)列出样本的频率分布表.
(2)画出频率分布直方图.
(3)根据频率分布表,估计数据落在[15.5,24.5)内的可能性约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com