【题目】(2018·邯郸一模)若甲、乙两类水果的质量(单位：kg)分别服从正态分布N(μ1，σ2)及N(μ2，σ2)，其正态分布的密度曲线如图所示，则下列说法错误的是( )
A. 乙类水果的质量服从的正态分布的参数σ2＝64
B. 甲类水果的质量比乙类水果的质量更集中
C. 甲类水果的平均质量μ1＝0.4 kg
D. 甲类水果的平均质量比乙类水果的平均质量小
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）如图，设直线
将坐标平面分成
四个区域（不含边界），若函数
的图象恰好位于其中一个区域内，判断其所在的区域并求对应的
的取值范围；
（2）当
时，求证：
且
，有
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了了解校园噪音情况，学校环保协会对校园噪音值（单位：分贝）进行了
天的监测，得到如下统计表：
噪音值（单位：分贝） |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
（1）根据该统计表，求这
天校园噪音值的样本平均数（同一组的数据用该组组间的中点值作代表）.
（2）根据国家声环境质量标准：“环境噪音值超过
分贝，视为重度噪音污染；环境噪音值不超过
分贝，视为度噪音污染.”如果把由上述统计表算得的频率视作概率，回答下列问题：
（i）求周一到周五的五天中恰有两天校园出现重度噪音污染而其余三天都是轻度噪音污染的概率.
（ii）学校要举行为期
天的“汉字听写大赛”校园选拔赛，把这
天校园出现的重度噪音污染天数记为
，求
的分布列和方差
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列抽取样本的方式属于简单随机抽样的个数为( )
①从无限多个个体中抽取100个个体作为样本.
②盒子里共有80个零件，从中选出5个零件进行质量检验.在抽样操作时，从中任意拿出一个零件进行质量检验后再把它放回盒子里.
③从20件玩具中一次性抽取3件进行质量检验.
④某班有56名同学，指定个子最高的5名同学参加学校组织的篮球赛.
A.0B.1C.2D.3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面
是平形四边形，设
，
平面，点
为
的中点，且
，
．
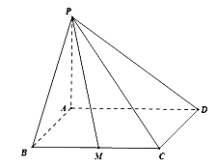
（1）若
，求二面角
的正切值；
（2）是否存在
使
，若存在求出，若不存在请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业2017年招聘员工，其中A、B、C、D、E五种岗位的应聘人数、录用人数和录用比例（精确到1%）如下：
（Ⅰ）从表中所有应聘人员中随机选择1人，试估计此人被录用的概率；
（Ⅱ）从应聘E岗位的6人中随机选择1名男性和1名女性，求这2人均被录用的概率；
（Ⅲ）表中A、B、C、D、E各岗位的男性、女性录用比例都接近（二者之差的绝对值不大于5%），但男性的总录用比例却明显高于女性的总录用比例．研究发现，若只考虑其中某四种岗位，则男性、女性的总录用比例也接近，请写出这四种岗位．（只需写出结论）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
，其中
，
，且
．
（1）当
时，函数
在
处的切线与直线
平行，试求m的值；
（2）当时，令
，若函数
有两个极值点
，且
，求
的取值范围；
（3）当
时，试讨论函数的零点个数，并证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的一系列对应值如下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）根据表格提供的数据求函数
的一个解析式；
（2）根据（1）的结果，若函数
周期为
，当
时，方程
恰有两个不同的解，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的离心率为
，且椭圆
过点
.过点
做两条相互垂直的直线
、
分别与椭圆
交于
、
、
、
四点.
（Ⅰ）求椭圆
的标准方程；
（Ⅱ）若
， 
，探究：直线
是否过定点？若是，请求出定点坐标；若不是，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
