
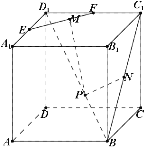
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点,
的中点,![]() 是线段
是线段![]() 的中点,若点
的中点,若点![]() 分别为线段
分别为线段![]() 上的动点,则
上的动点,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
连接B1D1交EF于G,连接PG,则EF⊥平面B1D1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D1G为D1B1的四分之一.其次,连接BD,设其中点为H,连接PH,BC1,则△D1DB≌△D1C1B,从而PN=PH.(实现了转化,这步是解题之关键),最后,连接GH交BD1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH,即可得出结论.
首先PM的最小值就是P到EF的距离.
连接B1D1交EF于G,连接PG,则EF⊥平面B1D1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D1G为D1B1的四分之一.其次,连接BD,设其中点为H,连接PH,BC1,则△D1DB≌△D1C1B1,从而PN=PH.(实现了转化,这步是解题之关键)
最后,连接GH交BD1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH.
∵正方体ABCD﹣A1B1C1D1的棱长为1,
∴GH=![]() =
=![]() .
.
故选:D.


科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是 ![]() ,过E的右焦点且垂直于椭圆长轴的直线与椭圆交于A,B两点,|AB|=2.
,过E的右焦点且垂直于椭圆长轴的直线与椭圆交于A,B两点,|AB|=2.
(Ⅰ)求椭圆方程;
(Ⅱ)过点P(0, ![]() )的动直线l与椭圆E交于的两点M,N(不是的椭圆顶点),是否存在实数λ,使
)的动直线l与椭圆E交于的两点M,N(不是的椭圆顶点),是否存在实数λ,使 ![]() +λ
+λ ![]() 为定值?若存在,求出λ的值;若不存在,请说明理由.
为定值?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数g(x)满足g(g(x))=n(n∈N)有n+3个解,则称函数g(x)为“复合n+3解”函数.已知函数f(x)= 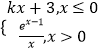 (其中e是自然对数的底数,e=2.71828…,k∈R),且函数f(x)为“复合5解”函数,则k的取值范围是( )
(其中e是自然对数的底数,e=2.71828…,k∈R),且函数f(x)为“复合5解”函数,则k的取值范围是( )
A.(﹣∞,0)
B.(﹣e,e)
C.(﹣1,1)
D.(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
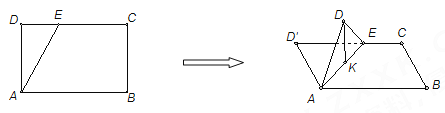
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上一动点,现将
上一动点,现将![]() 沿
沿![]() 折起,使点
折起,使点![]() 在面
在面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,当点
上,当点![]() 从
从![]() 运动到
运动到![]() ,则点
,则点![]() 所形成轨迹的长度为( )
所形成轨迹的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,倾斜角为α(α≠ ![]() )的直线l的参数方程为
)的直线l的参数方程为 ![]() (t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρcos2θ﹣4sinθ=0.
(t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρcos2θ﹣4sinθ=0.
(I)写出直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P(1,0).若点M的极坐标为(1, ![]() ),直线l经过点M且与曲线C相交于A,B两点,设线段AB的中点为Q,求|PQ|的值.
),直线l经过点M且与曲线C相交于A,B两点,设线段AB的中点为Q,求|PQ|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.
的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.
(I)若直线l1的倾斜角为 ![]() ,求△ABM的面积S的值;
,求△ABM的面积S的值;
(Ⅱ)过点B作直线BN⊥l于点N,证明:A,M,N三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
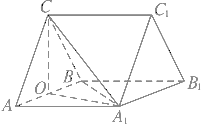
【题目】如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
O为AB的中点
(1)证明:AB⊥平面A1OC
(2)若AB=CB=2,平面ABC![]() 平面A1ABB1,求三棱柱ABC-A1B1C1的体积.
平面A1ABB1,求三棱柱ABC-A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x2017的方差是4,若yi=2xi﹣1(i=1,2,…,2017),则y1 , y2 , …y2017的方差为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com