解:(1)函数f(x)定义域为x>0,

=

.
由f'(x)>0且x>0
得
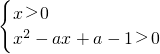
即

(i)当a-1=1即a=2时,f(x)在(0,+∞)上为增函数;
(ii)当a>2时,x>a-1或0<x<1,∴f(x)在(a-1,+∞),(0,1)上为增函数;
(iii)当1<a<2时,0<x<a-1或x>1,∴f(x)在(0,a-1),(1,+∞)上为增函数.
综上可知:f(x)的单调区间为:当a=2时,(0,+∞)
当a>2时,(a-1,+∞),(0,1)
当1<a<2时,(0,a-1),(1,+∞).
(2)x=2是f(x)极值点,∴f'(2)=0,即

,解得a=3.
∴

(x>0),

.
∵

,且当2<x<e
2时,f
′(x)>0;当1<x<2时,f
′(x)<0;当

时,f′(x)>0.
∴函数f(x)在区间

及(2,e
2]上单调递增,在区间(1,2)上单调递减.
∴f(x)在
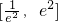
最大值应在x=1和x=e
2处取得
又
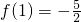
,

,
∴

.
分析:(1)利用f
′(x)>0即可求出其单调递增区间;
(2)利用函数取得极值点的条件先求出a的值,再利用导数得出其单调区间、极值,进而即可求出其最值.
点评:熟练掌握分类讨论的思想方法、利用导数研究函数的单调性与极值是解题的关键.

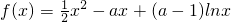 (a>1)
(a>1) =
= .
.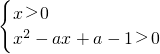 即
即
 ,解得a=3.
,解得a=3. (x>0),
(x>0), .
. ,且当2<x<e2时,f′(x)>0;当1<x<2时,f′(x)<0;当
,且当2<x<e2时,f′(x)>0;当1<x<2时,f′(x)<0;当 时,f′(x)>0.
时,f′(x)>0. 及(2,e2]上单调递增,在区间(1,2)上单调递减.
及(2,e2]上单调递增,在区间(1,2)上单调递减.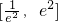 最大值应在x=1和x=e2处取得
最大值应在x=1和x=e2处取得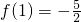 ,
, ,
, .
.

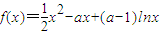 (a>1)
(a>1)