Question

设数列满足a₁=2，a_n+1-a_n=3•2^2n-1
（1）求数列{a_n}的通项公式；
（2）令b_n=na_n，求数列的前n项和S_n．

Answer 1

【答案】分析：（Ⅰ）由题意得a_n+1=[（a_n+1-a_n）+（a_n-a_n-1）+…+（a₂-a₁）]+a₁=3（2^2n-1+2^2n-3+…+2）+2=2^2（n+1）-1．由此可知数列{a_n}的通项公式为a_n=2^2n-1．
（Ⅱ）由b_n=na_n=n•2^2n-1知S_n=1•2+2•2³+3•2⁵++n•2^2n-1，由此入手可知答案．
解答：解：（Ⅰ）由已知，当n≥1时，a_n+1=[（a_n+1-a_n）+（a_n-a_n-1）+…+（a₂-a₁）]+a₁
=3（2^2n-1+2^2n-3+…+2）+2=2^2（n+1）-1．
而a₁=2，
所以数列{a_n}的通项公式为a_n=2^2n-1．
（Ⅱ）由b_n=na_n=n•2^2n-1知S_n=1•2+2•2³+3•2⁵+…+n•2^2n-1①
从而2²S_n=1•2³+2•2⁵+…+n•2²ⁿ⁺¹②
①-②得（1-2²）•S_n=2+2³+2⁵+…+2^2n-1-n•2²ⁿ⁺¹．
即．
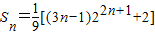
点评：本题主要考查数列累加法（叠加法）求数列通项、错位相减法求数列和等知识以及相应运算能力．
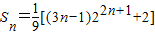