练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

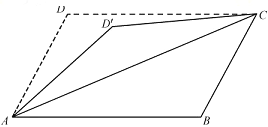
    【题目】如图，四边形ABCD为矩形，沿AB将△ADC翻折成.设二面角的平面角为，直线与直线BC所成角为，直线与平面ABC所成角为，当为锐角时，有

    A. B. C. D.

    【答案】B

    【解析】

    设三棱锥D-ABC是棱长为2的正四面体，取AB中点E，DC中点M，AC中点M，连结DE、CE、MN、EN，过D作DO⊥CE，交CE于O，连结AO，则，，由此能求出结果．

    设三棱锥D-ABC是棱长为2的正四面体，

    取AB中点E，DC中点M，AC中点M，连结DE、CE、MN、EN，过D作DO⊥CE，交CE于O，连结AO，则， ，DC=2，

    ∴， ，

    ∴，

    取BC中点E，连结DE、AE，则DE⊥BC，AE⊥BC，

    又，∴平面AED，∴．

    ∴．故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知向量函数的最小正周期为．

    （1）求函数的单调递增区间；

    （2）在中，角的对边分别是，且满足，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，（为常数），．曲线在点处的切线与轴平行

    （1）求的值；

    （2）求的单调区间和最小值；

    （3）若对任意恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】要建造一段长的高速公路，工程队需要把380名施工人员分为两组，一组负责的软土地带的施工，另一组完成剩下的硬土地带的施工.根据工程技术人员的测算，软、硬地带每米公路的工程量分别为50人·天和30人·天.

    （1）设参与软土地带工作的人数为人，试分别写出在软、硬地带筑路的时间关于的函数表达式；

    （2）问如何安排两组的人数，才能使全队筑路工期最短？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知．

    （Ⅰ）若函数在上单调递增，求实数的取值范围；

    （Ⅱ）若函数在区间上的最大值为，最小值为，令，求的解析式及其最小值（注：为自然对数的底数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】风景秀美的宝湖畔有四棵高大的银杏树，记作A，B，P，Q，湖岸部分地方围有铁丝网不能靠近．欲测量P，Q两棵树和A，P两棵树之间的距离，现可测得A，B两点间的距离为100 m，∠PAB＝75°，∠QAB＝45°，∠PBA＝60°，∠QBA＝90°，如图所示．则P，Q两棵树和A，P两棵树之间的距离各为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）若是的一个极值点，求函数表达式, 并求出的单调区间；

    （Ⅱ）若，证明当时，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的等腰梯形ABCD中，，，E为CD中点．若沿AE将三角形DAE折起，并连接DB，DC，得到如图所示的几何体D-ABCE，在图中解答以下问题：

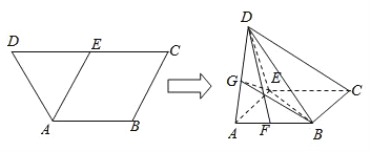
    （1）设G为AD中点，求证：平面GBE；

    （2）若平面平面ABCE，且F为AB中点，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数。

    （I）当时，证明：当时，；

    （II）若当时，恒成立，求a的取值范围。

    查看答案和解析>>

    同步练习册答案