
【题目】已知f(n)=1+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,g(n)=
,g(n)= ![]() ﹣
﹣ ![]() ,n∈N* .
,n∈N* .
(1)当n=1,2,3时,试比较f(n)与g(n)的大小关系;
(2)猜想f(n)与g(n)的大小关系,并给出证明.
【答案】
(1)解:当n=1时,f(1)=1,g(1)=1,所以f(1)=g(1);
当n=2时, ![]() ,
, ![]() ,
,
所以f(2)<g(2);
当n=3时, ![]() ,
, ![]() ,
,
所以f(3)<g(3)
(2)解:由(1),猜想f(n)≤g(n),下面用数学归纳法给出证明:
①当n=1,2,3时,不等式显然成立.
②假设当n=k(k≥3)时不等式成立,
即即 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() ,
,
那么,当n=k+1时, ![]() ,
,
因为 ![]() ,
,
所以 ![]() .
.
由①、②可知,对一切n∈N*,都有f(n)≤g(n)成立
【解析】(1)根据已知 ![]() ,
, ![]() ,n∈N* . 我们易得当n=1,2,3时,两个函数函数值的大小,比较后,根据结论我们可以归纳推理得到猜想f(n)≤g(n);(2)但归纳推理的结论不一定正确,我们可用数学归纳法进行证明,先证明不等式f(n)≤g(n)当n=1时成立,再假设不等式f(n)≤g(n)当n=k(k≥1)时成立,进而证明当n=k+1时,不等式f(n)≤g(n)也成立,最后得到不等式f(n)≤g(n)对于所有的正整数n成立;
,n∈N* . 我们易得当n=1,2,3时,两个函数函数值的大小,比较后,根据结论我们可以归纳推理得到猜想f(n)≤g(n);(2)但归纳推理的结论不一定正确,我们可用数学归纳法进行证明,先证明不等式f(n)≤g(n)当n=1时成立,再假设不等式f(n)≤g(n)当n=k(k≥1)时成立,进而证明当n=k+1时,不等式f(n)≤g(n)也成立,最后得到不等式f(n)≤g(n)对于所有的正整数n成立;


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,且△ABC为等边三角形,AA1=AB=6,D为AC的中点.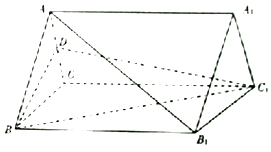
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面ACC1A1;
(3)求三棱锥C﹣BC1D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于棱锥、棱台的说法,其中不正确的是( )
A.棱台的侧面一定不会是平行四边形
B.棱锥的侧面只能是三角形
C.由四个面围成的封闭图形只能是三棱锥
D.棱锥被平面截成的两部分不可能都是棱锥
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )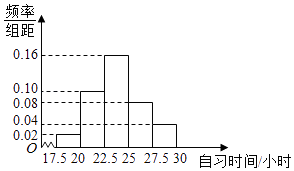
A.56
B.60
C.120
D.140
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx
(1)求f(x)在点(1,f(1))处的切线方程;
(2)若函数 ![]() 在[1,e]上的最小值为
在[1,e]上的最小值为 ![]() ,求a的值;
,求a的值;
(3)若k∈Z,且f(x)+x﹣k(x﹣1)>0对任意x>1恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=3cosx的图象,只需将函数y=3sin(2x﹣ ![]() )的图象上所有点的( )
)的图象上所有点的( )
A.横坐标缩短到原来的 ![]() (纵坐标不变),所得图象再向左平移
(纵坐标不变),所得图象再向左平移 ![]() 个单位长度
个单位长度
B.横坐标缩短到原来的 ![]() (纵坐标不变),所得图象再向右平移
(纵坐标不变),所得图象再向右平移 ![]() 个单位长度
个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移 ![]() 个单位长度
个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.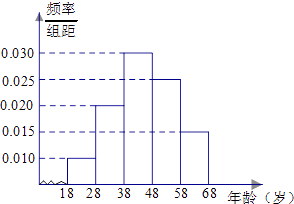
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个生物研究性学习小组,为了研究平均气温与一天内某豆类胚芽生长之间的关系,他们分别记录了4月6日至4月11日的平均气温x(℃)与该豆类胚芽一天生长的长度y(mm),得到如下数据:
日期 | 4月6日 | 4月7日 | 4月8日 | 4月9日 | 4月10日 | 4月11日 |
平均气温x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
一天生长的长度y(mm) | 22 | 25 | 29 | 26 | 16 | 12 |
该小组的研究方案是:先从这六组数据中选取6日和11日的两组数据作为检验数据,用剩下的4组数据即:7日至10日的四组数据求出线性回归方程.
(1)请按研究方案求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)用6日和11日的两组数据作为检验数据,并判断该小组所得线性回归方程是否理想.(若由线性回归方程得到的估计数据与所选的检验数据的误差不超过1mm,则认为该方程是理想的)
参考公式:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com