
【题目】已知![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆
是椭圆![]() 上一点,当
上一点,当![]() 时,有
时,有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点,试问在
两点,试问在![]() 铀上是否存在与
铀上是否存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立?若存在,求出定点
恒成立?若存在,求出定点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]()
(2)存在, T(4,0)
【解析】
(1)由题意,![]() .故
.故![]() .然后设点
.然后设点![]() 坐标为
坐标为![]() ,代入椭圆方程,联立椭圆定义
,代入椭圆方程,联立椭圆定义![]() ,进一步计算可得椭圆
,进一步计算可得椭圆![]() 的标准方程;
的标准方程;
(2)假设存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立,则
恒成立,则![]() ,设出
,设出![]() 、
、![]() 、
、![]() 点坐标代入
点坐标代入![]() 计算,可得
计算,可得![]() .然后设直线
.然后设直线![]() .联立直线与椭圆方程,消去
.联立直线与椭圆方程,消去![]() 整理可得一元二次方程,根据韦达定理有
整理可得一元二次方程,根据韦达定理有![]() ,
,![]() .然后代入
.然后代入![]() 进行计算可判断是否是定值,即可得到结论.
进行计算可判断是否是定值,即可得到结论.
解:(1)由题意,![]() .故
.故![]() .
.
可设点![]() 坐标为
坐标为![]() ,则
,则
![]() ,解得
,解得![]() ,即
,即![]() .
.
![]() ,解得
,解得![]() .
.
![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由题意,假设存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立,
恒成立,
设![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则
![]() ,
,![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
整理,得![]() .
.
设直线![]() .
.
联立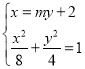 ,
,
消去![]() ,整理得
,整理得![]() .
.
![]()
![]() ,
,![]() .
.
![]()
![]() .
.
![]()
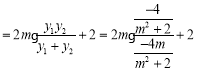
![]() .
.
![]() 存在与
存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立,且点
恒成立,且点![]() 坐标为
坐标为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】马林●梅森是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物,梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作,人们为了纪念梅森在数论方面的这一贡献,将形如2P﹣1(其中p是素数)的素数,称为梅森素数.若执行如图所示的程序框图,则输出的梅森素数的个数是( )
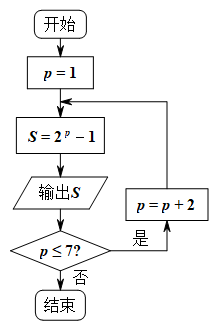
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=2px(p>0)的焦点为F,准线为l,AB为过焦点F且垂直于x轴的抛物线C的弦,已知以AB为直径的圆经过点(-1,0).
(1)求p的值及该圆的方程;
(2)设M为l上任意一点,过点M作C的切线,切点为N,证明:MF⊥NF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
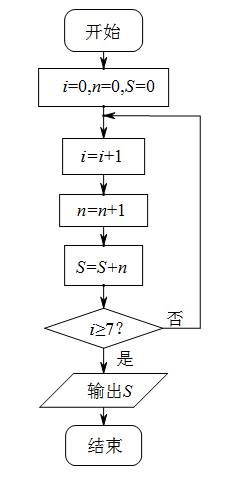
A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将编号为1,2,3,4,5,6,7的小球放入编号为1,2,3,4,5,6,7的七个盒子中,每盒放一球,若有且只有三个盒子的编号与放入的小球的编号相同,则不同的放法种数为( ).
A.5040B.24C.315D.840
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com