
【题目】甲、乙、丙三人投篮的命中率各不相同,其中乙的命中率是甲的2倍,丙的命中率等于甲与乙的命中率之和.若甲与乙各投篮一次,每人投篮相互独立,则他们都命中的概率为0.18.
(1)求甲、乙、丙三人投篮的命中率;
(2)现要求甲、乙、丙三人各投篮一次,假设每人投篮相互独立,记三人命中总次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附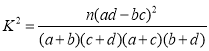 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术,通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍,若在正方形图案上随机取一点,则该点取自白色区域的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 的两顶点坐标
的两顶点坐标![]() ,
,![]() ,圆
,圆![]() 是
是![]() 的内切圆,在边
的内切圆,在边![]() ,
,![]() ,
,![]() 上的切点分别为
上的切点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
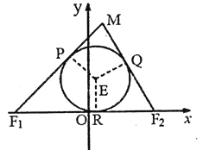
(Ⅰ)求证:![]() 为定值,并求出动点
为定值,并求出动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过![]() 的斜率不为零直线交曲线
的斜率不为零直线交曲线![]() 于
于![]() 、
、![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为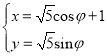 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)求C1的极坐标方程;
(2)若C1与曲线C2:ρ=2sinθ交于A,B两点,求|OA||OB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() (任意项都不为零)的前
(任意项都不为零)的前![]() 项和为
项和为![]() ,首项为
,首项为![]() ,对于任意
,对于任意![]() ,满足
,满足![]() .
.
(1)数列![]() 的通项公式;
的通项公式;
(2)是否存在![]() 使得
使得![]() 成等比数列,且
成等比数列,且![]() 成等差数列?若存在,试求
成等差数列?若存在,试求![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设数列![]() ,
, ,若由
,若由![]() 的前
的前![]() 项依次构成的数列是单调递增数列,求正整数
项依次构成的数列是单调递增数列,求正整数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 右焦点为
右焦点为![]() ,右准线l的方程为
,右准线l的方程为![]() ,过焦点F的直线与椭圆C相交于点A,B(不与点
,过焦点F的直线与椭圆C相交于点A,B(不与点![]() 重合).
重合).
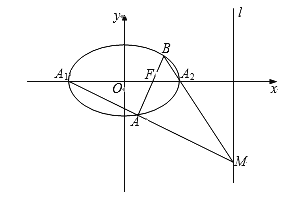
(1)求椭圆C的标准方程;
(2)当直线AB的倾斜角为45°时,求弦AB的长;
(3)设直线![]() 交l于点M,求证:B,
交l于点M,求证:B,![]() ,M三点共线.
,M三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省2020年高考将实施新的高考改革方案.考生的高考总成绩由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、政治、历史、地理6科中选择3门作为选考科目,语文、数学、外语三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%.等级考试科目成绩计入考生总成绩时,将
共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%.等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到91~100,81~90,71~80,61~70,51~60,41~50,31~40,21~30八个分数区间,得到考生的等级成绩.举例说明:某同学化学学科原始分为65分,该学科
等级内的考生原始成绩,依照等比例转换法则,分别转换到91~100,81~90,71~80,61~70,51~60,41~50,31~40,21~30八个分数区间,得到考生的等级成绩.举例说明:某同学化学学科原始分为65分,该学科![]() 等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属
等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为61~70,那么该同学化学学科的转换分计算方法为:设该同学化学学科的转换等级分为
等级的转换分区间为61~70,那么该同学化学学科的转换分计算方法为:设该同学化学学科的转换等级分为![]() ,
,![]() ,求得
,求得![]() .四舍五入后该同学化学学科赋分成绩为67.为给高一学生合理选科提供依据,全省对六个选考科目进行测试,某校高一年级2000人,根据该校高一学生的物理原始成绩制成频率分布直方图(见右图).由频率分布直方图,可以认为该校高一学生的物理原始成绩
.四舍五入后该同学化学学科赋分成绩为67.为给高一学生合理选科提供依据,全省对六个选考科目进行测试,某校高一年级2000人,根据该校高一学生的物理原始成绩制成频率分布直方图(见右图).由频率分布直方图,可以认为该校高一学生的物理原始成绩![]() 服从正态分布
服从正态分布![]() ,用这2000名学生的平均物理成绩
,用这2000名学生的平均物理成绩![]() 作为
作为![]() 的估计值,用这2000名学生的物理成绩的方差
的估计值,用这2000名学生的物理成绩的方差![]() 作为
作为![]() 的估计值.
的估计值.
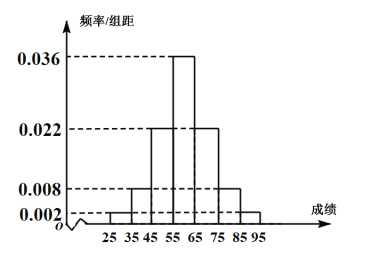
(1)若张明同学在这次考试中的物理原始分为86分,等级为![]() ,其所在原始分分布区间为82~93,求张明转换后的物理成绩(精确到1);按高考改革方案,若从全省考生中随机抽取100人,记
,其所在原始分分布区间为82~93,求张明转换后的物理成绩(精确到1);按高考改革方案,若从全省考生中随机抽取100人,记![]() 表示这100人中等级成绩在区间
表示这100人中等级成绩在区间![]() 内的人数,求
内的人数,求![]() 最有可能的取值(概率最大);
最有可能的取值(概率最大);
(2)①求![]() ,
,![]() (同一组中的数据用该组区间的中点作代表);
(同一组中的数据用该组区间的中点作代表);
②由①中的数据,记该校高一学生的物理原始分高于84分的人数为![]() ,求
,求![]() .
.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com