
分析 (1)根据复合函数f(log3x)=0可得${log_3}x-\frac{1}{{{{log}_3}x}}=0$,利用换元法,设t=log3x即可求解.
(2)根据复合函数,由已知,m≠0,$mx-\frac{1}{mx}+m(x-\frac{1}{x})<0$,分离参数,讨论可得实数m的取值范围;
(3)根据log2f(x)=log2(ax+1)转化为$x-\frac{1}{x}=ax+1$,根据$x-\frac{1}{x}>0$求出-1<x<0或x>1,问题转化为关于x的方程$x-\frac{1}{x}=ax+1$在区间(-1,0)∪(1,+∞)有且只有一个解,即方程(a-1)x2+x+1=0在(-1,0)∪(1,+∞)有且只有一个解.对a进行讨论即可.
解答 解:(1)∵f(log3x)=0
∴${log_3}x-\frac{1}{{{{log}_3}x}}=0$,
设t=log3x,
可得$t-\frac{1}{t}=0$,即$\frac{{{t^2}-1}}{t}=0$
解得:t=1或t=-1
故得x=3或$x=\frac{1}{3}$.
(2)由已知,m≠0,$mx-\frac{1}{mx}+m(x-\frac{1}{x})<0$
∵x∈[1,+∞)
∴$m{x^2}-\frac{1}{m}+m{x^2}-m<0$
∴$2m{x^2}<\frac{1}{m}+m$
(1)当m>0时,${x^2}<\frac{1}{2}+\frac{1}{{2{m^2}}}$,∴对任意x∈[1+∞),此式不能恒成立;
(2)当m<0时,${x^2}>\frac{1}{2}+\frac{1}{{2{m^2}}}$;
∵x∈[1+∞),可得x2min=1,
∴$1>\frac{1}{2}+\frac{1}{{2{m^2}}}$
∴m2>1
∵m<0
∴m<-1
综上:m<-1.
(3)∵log2f(x)=log2(ax+1)
∴$x-\frac{1}{x}=ax+1$
∵$x-\frac{1}{x}>0$
∴-1<x<0或x>1
本问题转化为关于x的方程$x-\frac{1}{x}=ax+1$在区间(-1,0)∪(1,+∞)有且只有一个解,
即方程(a-1)x2+x+1=0在(-1,0)∪(1,+∞)有且只有一个解.
(1)当a=1时,x=-1不满足题意.
(2)当a>1时,设g(x)=(a-1)x2+x+1,开口向上,对称轴$x=-\frac{1}{2(a-1)}<0$,
①当△=0时,即$a=\frac{5}{4}$时,此时x=-2不满足题意.
②当△<0时,即$a>\frac{5}{4}$时,此时方程无解,不满足题意.
③当△>0时,即$1<a<\frac{5}{4}$时,g(-1)=a-1>0,则两根均在(-1,0)或均在(1,+∞),不满足题意.
(3)当a<1时,设g(x)=(a-1)x2+x+1,开口向下,对称轴$x=-\frac{1}{2(a-1)}>0$,
∵g(0)=1>0,g(-1)=a-1<0,
∴存在x0∈(-1,0)使g(x0)=0,若满足题意,另一根必在(0,1]内,
∴g(1)≤0,即a+1≤0,
∴a≤-1
综上可得:a≤-1.即a的取值范围时(-∞,-1].
点评 本题考查了对数的计算,二次函数的系数的讨论和恒成立问题的转化.分离参数的求解.属于难题.


科目:高中数学 来源: 题型:填空题
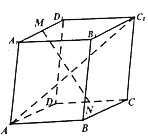 已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.
已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=84x | B. | y=21(1+4x) | C. | y=21x4 | D. | y=21(1+x)4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
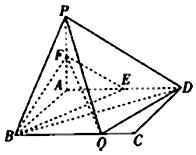 如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.
如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com