
分析 (1)求出函数的对称轴,求得端点处的函数值,即可得到最值;
(2)求出导数,求出极值和端点处的函数值,即可得到最值;
(3)求出对称轴,判断区间的单调性,即可得到最值;
(4)求出导数,求出极值和端点的函数值,即可得到最值.
解答 解:(1)f(x)=6x2+x+2的对称轴为x=-$\frac{1}{12}$∈[-1,1],
即有最小值为f(-$\frac{1}{12}$)=$\frac{47}{24}$,最大值为f(1)=9;
(2)f(x)=x3-12x的导数为f′(x)=3x2-12,
由f′(x)=0解得x=±2,
由f(-2)=16,f(2)=-16,f(-3)=9,f(3)=-9,
即有最大值为16,最小值为-16;
(3)f(x)=6-12x+x2的对称轴为x=6,
区间[-$\frac{1}{3}$,1]为减区间,即有f(1)取得最小值,且为-5;
f(-$\frac{1}{3}$)=$\frac{91}{9}$;
(4)f(x)=48x-x3的导数为f′(x)=48-3x2,
由f′(x)=0解得x=±4(-4舍去),
由f(4)=128,f(-3)=-117,f(5)=115.
即有最小值为-117,最大值为128.
点评 本题考查函数的最值的求法,注意运用导数和单调性的运用,考查运算能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | P<Q | B. | P>Q | C. | P=Q | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
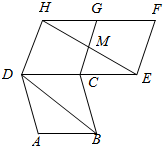 如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )
如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )| A. | |$\overrightarrow{AB}$|=|$\overrightarrow{EF}$| | B. | $\overrightarrow{AB}$与$\overrightarrow{FH}$共线 | C. | $\overrightarrow{BD}$与$\overrightarrow{EH}$共线 | D. | $\overrightarrow{DC}$与$\overrightarrow{EC}$共线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$<a≤$\frac{1}{2}$ | B. | $\frac{1}{3}$≤a<$\frac{1}{2}$ | ||
| C. | $\frac{1}{3}$<a≤$\frac{1}{2}$或-$\frac{1}{2}$≤a<-$\frac{1}{3}$ | D. | $\frac{1}{3}$≤a<$\frac{1}{2}$或-$\frac{1}{2}$<a≤-$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com