
【题目】已知![]() ,
,![]() ,对任意
,对任意![]() ,有
,有![]() 成立.
成立.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() ,
,![]() 恒成立;
恒成立;
(3)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意
项和,若对任意![]() 均有
均有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]()
【解析】
(1)由![]() 可得
可得![]() ,结合平面向量的坐标运算可得到
,结合平面向量的坐标运算可得到![]() 的关系式,再结合
的关系式,再结合![]() 可证明数列
可证明数列![]() 是等比数列,进而可求出通项公式;
是等比数列,进而可求出通项公式;
(2)将![]() 两端同时除以
两端同时除以![]() ,可得到
,可得到![]() ,从而可证明数列
,从而可证明数列![]() 是等差数列,即可求出
是等差数列,即可求出![]() 的表达式,进而求得
的表达式,进而求得![]() 的通项公式,通过判断其表达式特点,可求出满足题意的正整数
的通项公式,通过判断其表达式特点,可求出满足题意的正整数![]() ;
;
(3)由题得,![]() ,利用裂项相消求和法可求出
,利用裂项相消求和法可求出![]() ,结合不等式的性质,可求出
,结合不等式的性质,可求出![]() 的最小值.
的最小值.
(1)由题可得![]() ,则
,则![]() ,
,
当![]() 时,可得
时,可得![]() .
.
![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,
,
故数列![]() 是以2为首项,公比为2的等比数列,通项公式为
是以2为首项,公比为2的等比数列,通项公式为![]() .
.
(2)![]() ,等式两端同时除以
,等式两端同时除以![]() 得:
得:![]() ,即
,即![]() ,
,
故![]() 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列,通项公式为
的等差数列,通项公式为![]() ,
,
则![]() .
.
因为当![]() ,
,![]() ,当
,当![]() 时
时![]() ,
,![]() ,所以当
,所以当![]() 或
或![]() 时,
时,![]() 取最大值,对任意
取最大值,对任意![]() ,
,![]() 恒成立.
恒成立.
(3)由题意,![]() ,
,
则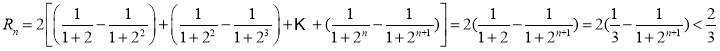 ,故
,故![]() .
.
所以![]() 的最小值为
的最小值为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某大型商场在2018年国庆举办了一次抽奖活动抽奖箱里放有3个红球,3个黑球和1个白球![]() 这些小球除颜色外大小形状完全相同
这些小球除颜色外大小形状完全相同![]() ,从中随机一次性取3个小球,每位顾客每次抽完奖后将球放回抽奖箱活动另附说明如下:
,从中随机一次性取3个小球,每位顾客每次抽完奖后将球放回抽奖箱活动另附说明如下:
![]() 凡购物满
凡购物满![]() 含
含![]() 元者,凭购物打印凭条可获得一次抽奖机会;
元者,凭购物打印凭条可获得一次抽奖机会;
![]() 凡购物满
凡购物满![]() 含
含![]() 元者,凭购物打印凭条可获得两次抽奖机会;
元者,凭购物打印凭条可获得两次抽奖机会;
![]() 若取得的3个小球只有1种颜色,则该顾客中得一等奖,奖金是一个10元的红包;
若取得的3个小球只有1种颜色,则该顾客中得一等奖,奖金是一个10元的红包;
![]() 若取得的3个小球有3种颜色,则该顾客中得二等奖,奖金是一个5元的红包;
若取得的3个小球有3种颜色,则该顾客中得二等奖,奖金是一个5元的红包;
![]() 若取得的3个小球只有2种颜色,则该顾客中得三等奖,奖金是一个2元的红包.
若取得的3个小球只有2种颜色,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据![]() 单位:元
单位:元![]() ,绘制得到如图所示的茎叶图.
,绘制得到如图所示的茎叶图.

![]() 求这20位顾客中获得抽奖机会的顾客的购物消费数据的中位数与平均数
求这20位顾客中获得抽奖机会的顾客的购物消费数据的中位数与平均数![]() 结果精确到整数部分
结果精确到整数部分![]() ;
;
![]() 记一次抽奖获得的红包奖金数
记一次抽奖获得的红包奖金数![]() 单位:元
单位:元![]() 为X,求X的分布列及数学期望,并计算这20位顾客在抽奖中获得红包的总奖金数的平均值
为X,求X的分布列及数学期望,并计算这20位顾客在抽奖中获得红包的总奖金数的平均值![]() 假定每位获得抽奖机会的顾客都会去抽奖
假定每位获得抽奖机会的顾客都会去抽奖![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定正整数![]() ,已知用克数都是正整数的
,已知用克数都是正整数的![]() 块砝码和一台天平可以称出质量为
块砝码和一台天平可以称出质量为![]() 克的所有物品.
克的所有物品.
(1)求![]() 的最小值
的最小值![]() ;
;
(2)当且仅当![]() 取什么值时,上述
取什么值时,上述![]() 块砝码的组成方式是惟一确定的?并证明你的结论.
块砝码的组成方式是惟一确定的?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=![]() ,M为BC的中点.
,M为BC的中点.

(I)证明:AM⊥PM ;
(II)求二面角P-AM-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.

(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com