思路分析:可以按逐一相加的程序进行,也可以运用公式1+2+3+…+n=
直接运算.由此得到下面的算法及相应的流程图.?
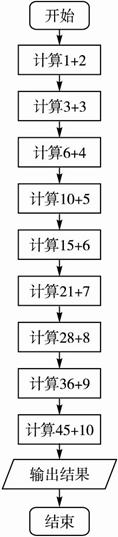
解:算法1:?
第一步:计算1+2得到结果3;?
第二步:将上一步中的运算结果3与3相加得到结果6;?
第三步:将上一步中的运算结果6与4相加得到结果10;?
第四步:将上一步中的运算结果10与5相加得到结果15;?
第五步:将上一步中的运算结果15与6相加得到结果21;?
第六步:将上一步中的运算结果21与7相加得到结果28;?
第七步:将上一步中的运算结果28与8相加得到结果36;?
第八步:将上一步中的运算结果36与9相加得到结果45;?
第九步:将上一步中的运算结果45与10相加得到结果55;?
第十步:输出运算结果.?
相应的流程图如图(1)所示.?
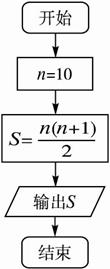
(1)算法2:?
第一步:取n=10;?
第二步:计算
;?
第三步:输出运算结果.?
相应的流程图如图(2)所示.?
(2)思维启示:两种算法的优劣是显而易见的,流程图的繁简也是非常明显的.算法1采用逐一相加的方法,需要10步,做了9步运算,人工输出9次,流程图用了10个图框,而算法2采用了利用公式的方法,只用了3步,人工输入了2次.可见在设计解决问题的算法时,需考虑多种算法,从中选出最优的、最简单的、最易于计算机执行、人工操作尽量少的算法,这一点是非常重要的.比如当本问题的加数增加到1 000时,再用算法1显然是不可行的.因为它太繁琐,而用算法2则不受加数多少的限制.因此在解决问题时,如果有或能总结出解决问题的公式,我们要尽量采用公式算法.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
| x | 1 | 2 | 3 | 4 |
| f（x） | 2 | 3 | 4 | 1 |
| x | 1 | 2 | 3 | 4 |
| g（x） | 2 | 1 | 4 | 3 |
查看答案和解析>>
科目：高中数学 来源： 题型：
| x |
1 | 2 | 3 | 4 | x |
1 | 2 | 3 | 4 |
| f（x） |
2 | 3 | 4 | 1 | g（x） |
2 | 1 | 4 | 3 |
查看答案和解析>>
科目：高中数学 来源： 题型：
| X | 10 | 11.3 | 11.8 | 12.5 | 13 |
| Y | 1 | 2 | 3 | 4 | 5 |
| U | 10 | 11.3 | 11.8 | 12.5 | 13 |
| V | 5 | 4 | 3 | 2 | 1 |
| A、r2＜r1＜0 |
| B、0＜r2＜r1 |
| C、r2＜0＜r1 |
| D、r2=r1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com