
四棱锥 中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 .已知
.已知 ,
, ,
, ,
, .
.

(Ⅰ)证明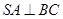 ;
;
(Ⅱ)求直线 与平面
与平面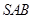 所成角的正弦值.
所成角的正弦值.
(Ⅰ)见解析.(Ⅱ)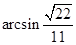
【解析】
试题分析:(Ⅰ)通过作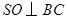 ,垂足为
,垂足为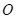 ,连结
,连结 ,根据侧面
,根据侧面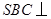 底面
底面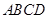 ,得
,得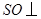 底面
底面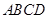 .应用三垂线定理,得
.应用三垂线定理,得 .(Ⅱ)立体几何中的角的计算,一般有两种思路,一是直接法,通过“一作,二证,三计算”等步骤,计算角;二是“间接法”,如利用图形与其投影的面积关系,确定角.本题首先设
.(Ⅱ)立体几何中的角的计算,一般有两种思路,一是直接法,通过“一作,二证,三计算”等步骤,计算角;二是“间接法”,如利用图形与其投影的面积关系,确定角.本题首先设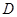 到平面
到平面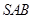 的距离为
的距离为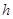 ,根据
,根据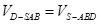 ,求得
,求得 .进一步确定
.进一步确定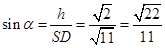 ,将角用反正弦函数表示.
,将角用反正弦函数表示.
试题解析:(Ⅰ)作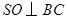 ,垂足为
,垂足为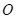 ,连结
,连结 ,由侧面
,由侧面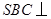 底面
底面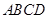 ,得
,得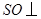 底面
底面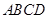 .
.
因为 ,所以
,所以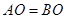 ,
,
又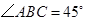 ,故
,故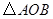 为等腰直角三角形,
为等腰直角三角形,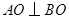 ,
,
由三垂线定理,得 .
.

(Ⅱ)由(Ⅰ)知 ,依题设
,依题设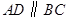 ,
,
故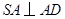 ,由
,由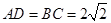 ,
,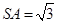 ,
, ,得
,得
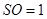 ,
, .
.
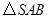 的面积
的面积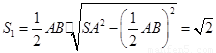 .
.
连结 ,得
,得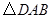 的面积
的面积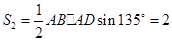
设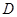 到平面
到平面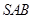 的距离为
的距离为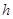 ,由于
,由于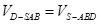 ,得
,得
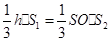 ,
,
解得 .
.
设 与平面
与平面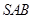 所成角为
所成角为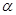 ,则
,则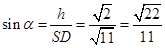 .
.
所以,直线 与平面
与平面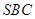 所成的角为
所成的角为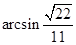
考点:垂直关系、平行关系,角的计算.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源:黑龙江省牡丹江一中10-11学年高一下学期期末考试数学(理) 题型:解答题
(本小题满分12分)如图,四棱锥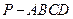 中,底面
中,底面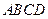 为平行四边形,
为平行四边形,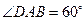 ,
,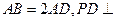 底面
底面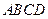 .
.
(1)证明: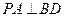 ;
;
(2)若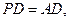 求二面角
求二面角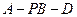 的余弦值.
的余弦值.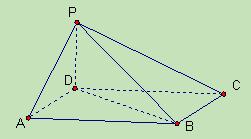
查看答案和解析>>
科目:高中数学 来源:2014届山西省高二10月月考国际班数学试卷(解析版) 题型:解答题
(本小题12分)
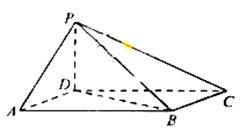
如图,四棱锥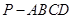 中,底面
中,底面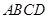 为平行四边形
为平行四边形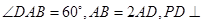 底面
底面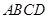
(I)证明: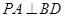
(II)设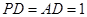 ,求棱锥
,求棱锥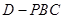 的高.
的高.
查看答案和解析>>
科目:高中数学 来源:2013届山东冠县武训高中高二下学期模块考试理科数学试卷(解析版) 题型:解答题
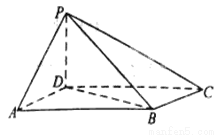
如图,四棱锥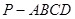 中,底面
中,底面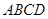 为平行四边形,
为平行四边形,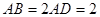 ,
,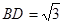 ,
,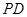 ⊥底面
⊥底面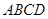 .
.
(1)证明:平面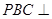 平面
平面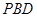 ;
;
(2)若二面角 为
为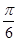 ,求
,求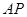 与平面
与平面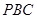 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省五校高三第三次联考理科数学(解析版) 题型:解答题
如图,在四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, 底面
底面 ,
, ,
, ,
, ,
, ,E在棱
,E在棱 上, (Ⅰ) 当
上, (Ⅰ) 当 时,求证:
时,求证: 平面
平面 ; (Ⅱ)
当二面角
; (Ⅱ)
当二面角 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三上学期2月月考理科数学试卷 题型:解答题
如图,四棱锥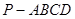 中,底面
中,底面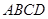 为平行四边形,
为平行四边形,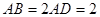 ,
,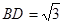 ,
,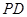 ⊥底面
⊥底面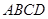 .
.
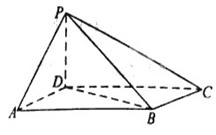
(1)证明:平面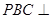 平面
平面 ;
;
(2)若二面角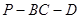 为
为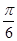 ,求
,求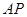 与平面
与平面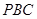 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com