
【题目】已知数列![]() 的首项
的首项![]() (
(![]() 是常数,且
是常数,且![]() ),
),![]()
![]() ,数列
,数列![]() 的首项
的首项![]() ,
,![]()
![]() .
.
(1)证明:![]() 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() 是等比数列,求实数
是等比数列,求实数![]() 的值;
的值;
(3)当![]() 时,求数列
时,求数列![]() 的最小项.
的最小项.
【答案】(1)证明见解析;(2)![]() ;
;
(3)当![]() 时,最小项为
时,最小项为![]() ;
;
当![]() 时,最小项为
时,最小项为![]() 或
或![]() ;
;
当![]() 时,最小项为
时,最小项为![]() ;
;
当![]() 时,最小项为
时,最小项为![]() 或
或![]() ;
;
当![]() 时,最小项为
时,最小项为![]() .
.
【解析】
(1)对![]() 进行化简,代入
进行化简,代入![]() ,然后得到与
,然后得到与![]() 的关系,得到
的关系,得到![]() 从第2项起是以2为公比的等比数列;(2)先得到
从第2项起是以2为公比的等比数列;(2)先得到![]() 的表达式,然后得到
的表达式,然后得到![]() ,根据
,根据![]() 是等比数列,得到
是等比数列,得到![]() 的方程,求出
的方程,求出![]() 的值;(3)根据得到的
的值;(3)根据得到的![]() 的通项,分类讨论,得到
的通项,分类讨论,得到![]() 中的最小项.
中的最小项.
解:(1)![]()
![]()
![]()
![]()
![]()
由![]() ,得
,得![]() ,
,![]()
![]() ,
,![]()
即![]() 从第2项起是以2为公比的等比数列.
从第2项起是以2为公比的等比数列.
(2)![]()
![]()
当![]() 时,
时,![]()
![]()
![]() 是等比数列,
是等比数列,
![]() 是常数,
是常数,![]() ,
,
即![]()
(3)由(1)知当![]() 时,
时,![]() ,
,
所以![]() ,
,
所以数列![]() 为
为![]()
显然最小项是前三项中的一项.
当![]() 时,最小项为
时,最小项为![]() ;
;
当![]() 时,最小项为
时,最小项为![]() 或
或![]() ;
;
当![]() 时,最小项为
时,最小项为![]() ;
;
当![]() 时,最小项为
时,最小项为![]() 或
或![]() ;
;
当![]() 时,最小项为
时,最小项为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】房屋的天花板上点![]() 处有一光源,
处有一光源,![]() 在地面上的射影为
在地面上的射影为![]() ,在地面上放置正棱锥
,在地面上放置正棱锥![]() ,底面
,底面![]() 接触地面.已知正四棱锥
接触地面.已知正四棱锥![]() 的高为
的高为![]() ,底面
,底面![]() 的边长为
的边长为![]() ,
,![]() 与正方形
与正方形![]() 的中心
的中心![]() 的距离为
的距离为![]() ,又
,又![]() 长为
长为![]() ,则棱锥影子(不包括底面
,则棱锥影子(不包括底面![]() )的面积的最大值为________.
)的面积的最大值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中,![]() ,若
,若![]() (
(![]() 为常数),则称
为常数),则称![]() 为“等差比数列”.下列是对“等差比数列”的判断:
为“等差比数列”.下列是对“等差比数列”的判断:
①![]() 不可能为
不可能为![]() ;②等差数列一定是等差比数列;
;②等差数列一定是等差比数列;
③等比数列一定是等差比数列;④等差比数列中可以有无数项为![]() .
.
其中正确的判断是( ).
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015全国高考试题)某公司为了解用户对其产品的满意度,从![]() ,
,![]() 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
![]() 地区:62 73 81 92 95 85 74 64 53 76
地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
![]() 地区:73 83 62 51 91 46 53 73 64 82
地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
根据用户满意度评分,将用户的满意度从低到高分为三个不同等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件![]() :“
:“![]() 地区用户的满意度等级高于
地区用户的满意度等级高于![]() 地区用户的满意度等级”假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求
地区用户的满意度等级”假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意,仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了![]() ,
,![]() 两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对
两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对![]() ,
,![]() 两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
|
| |
男业主 | 35 | 15 |
女业主 | 25 | 25 |
(1)分别估计![]() ,
,![]() 方案获得业主投票的概率;
方案获得业主投票的概率;
(2)判断能否有95%的把握认为投票选取管理方案与性别有关.
附: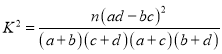 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,其前n项的积为
的各项均为正数,其前n项的积为![]() ,记
,记![]() ,
,![]() .
.
(1)若数列![]() 为等比数列,数列
为等比数列,数列![]() 为等差数列,求数列
为等差数列,求数列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求数列![]() 的通项公式.
的通项公式.
②记![]() ,那么数列
,那么数列![]() 中是否存在两项
中是否存在两项![]() ,(s,t均为正偶数,且
,(s,t均为正偶数,且![]() ),使得数列
),使得数列![]() ,
,![]() ,
,![]() ,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com