练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知α为锐角，则“sinα＞
    1
    3
    且cosα＞
    1
    3
    ”是“sin2α＞
    4
    		2
    9
    ”的（　　）
    分析：由题意可得，满足α1＜α＜α2且α1+α2=
    1
    2
    π    时0＜2α1＜2α＜2α2＜π且2α1+2α2=π，而sin2α1=2sinα1cosα1=
    4
    		2
    9
    ，可得sin2α＞
    4
    		2
    9
    ，可判断
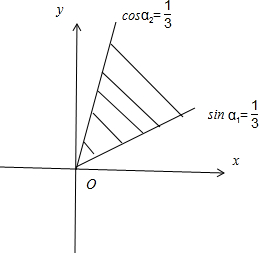    解答：解：∵α为锐角，且sinα＞
    1
    3
    且cosα＞
    1
    3

    ∴α的终边位置为如图所示的阴影区域的部分
    ∴α1＜α＜α2且α1+α2=
    1
    2
    π
    ∴0＜2α1＜2α＜2α2＜π且2α1+2α2=π
    ∴sin2α1=sin2α2
    ∵sinα1=
    1
    3

    ∴cosα1=
    2
    		2
    3

    ∴sin2α1=2sinα1cosα2=
    4
    		2
    9

    ∴sin2α＞
    4
    		2
    9

    由于α为锐角，以上的过程可逆
    ∴sinα＞
    1
    3
    且cosα＞
    1
    3
    是sin2α＞
    4
    		2
    9
    的充分必要条件
    故选A
    点评：本题主要考查了充分条件与必要条件的判断，解题的关键是灵活利用三角函数的性质，具有一定的综合性
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在锐角△ABC中，角A、B、C所对的边分别是a、b、c，已知S△ABC=
    3
    2
    		3
    ，且b=2，c=3，O为△ABC的外心，则
    OB
    •
    OC
    =
    -
    7
    6
    -
    7
    6
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：008

    判断正误:

    已知二面角M-l-N的大小为α(α是锐角), △ABC在面M内, 其面积为S,

     △A＇B＇C＇是△ABC在面N内的射影, 则△A＇B＇C＇的面积为S·cosα.

    (　　)

    查看答案和解析>>

    科目：高中数学 来源：聊城一中高一周考　任意角的三角函数　同角三角函数的基本关系式 题型：013

    已知锐角α终边上一点的坐标为(2sin3，－2cos3)，则α＝s

    [　　]
    A．

    π－3

    B．

    3

    C．

    3－

    D．

    －3

    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库二(有详细答案)人教版 人教版 题型：022

    已知二面角α－l－α的大小为(是锐角)，A∈l，B∈l，，且P∈α，P在β内的射影为．记△ABP的面积为S，则△AB的面积等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知，，S△ABC = ，且∠A是锐角，则·的值为（   ）

    A  －2           B ±2              C  2             D 4

    查看答案和解析>>

    同步练习册答案