
【题目】如图,矩形![]() 所在的半平面和直角梯形
所在的半平面和直角梯形![]() 所在的半平面成
所在的半平面成![]() 的二面角,
的二面角,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
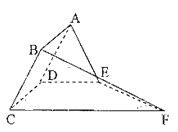
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使锐二面角
,使锐二面角![]() 的余弦值为
的余弦值为![]() .若存在,请求出
.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳含量达到了危险状态,经抢修,排气扇恢复正常.排气![]() 后,测得车库内的一氧化碳浓度为
后,测得车库内的一氧化碳浓度为![]() ,继续排气
,继续排气![]() ,又测得浓度为
,又测得浓度为![]() ,经检测知该地下车库一氧化碳浓度
,经检测知该地下车库一氧化碳浓度![]() 与排气时间
与排气时间![]() 存在函数关系:
存在函数关系: (
(![]() ,
,![]() 为常数)。
为常数)。
(1)求![]() ,
,![]() 的值;
的值;
(2)若地下车库中一氧化碳浓度不高于![]() 为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆过原点
为圆心的圆过原点![]() .
.
(1)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,若
,若![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)在(1)的条件下,设![]() ,且
,且![]() 分别是直线
分别是直线![]() 和圆
和圆![]() 上的动点,求
上的动点,求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等,![]() 是棱
是棱![]() 上的点(不含端点),记直线
上的点(不含端点),记直线![]() 与直线
与直线![]() 所成角为
所成角为![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用6个字母![]() 编拟某种信号程序(大小写有区别),把这6个字母全部排列如图所示的表格中,每个字母必须使用且只使用一次,不同的排列方式表示不同的信号,如果恰有一对字母(同一个字母的大小写)排到同一列的上下格位置,那么称此信号为“微错号”,则不同的“微错号”的总数为( )
编拟某种信号程序(大小写有区别),把这6个字母全部排列如图所示的表格中,每个字母必须使用且只使用一次,不同的排列方式表示不同的信号,如果恰有一对字母(同一个字母的大小写)排到同一列的上下格位置,那么称此信号为“微错号”,则不同的“微错号”的总数为( )
A.144B.288C.432D.576
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两个不重合的平面,下列选项中,一定能得出平面
是两个不重合的平面,下列选项中,一定能得出平面![]() 与平面
与平面![]() 平行的是( )
平行的是( )
A.平面![]() 内有一条直线与平面
内有一条直线与平面![]() 平行
平行
B.平面![]() 内有两条直线与平面
内有两条直线与平面![]() 平行
平行
C.平面![]() 内有一条直线与平面
内有一条直线与平面![]() 内的一条直线平行
内的一条直线平行
D.平面![]() 与平面
与平面![]() 不相交
不相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() (
(![]() ,
,![]() ,p为常数),则
,p为常数),则![]() 称为“等方差数列”.下列对“等方差数列”的判断,其中正确的为( )
称为“等方差数列”.下列对“等方差数列”的判断,其中正确的为( )
A.若![]() 是等方差数列,则
是等方差数列,则![]() 是等差数列
是等差数列
B.若![]() 是等方差数列,则
是等方差数列,则![]() 是等方差数列
是等方差数列
C.![]() 是等方差数列
是等方差数列
D.若![]() 是等方差数列,则
是等方差数列,则![]() (
(![]() ,k为常数)也是等方差数列
,k为常数)也是等方差数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com