
【题目】已知直线l经过直线3x+4y﹣2=0与直线2x+y+2=0的交点P,且垂直于直线x﹣2y﹣1=0.
(1)求直线l的方程;
(2)求直线l关于原点O对称的直线方程.
【答案】
(1)解:由 ![]() ,解得
,解得 ![]() ,
,
∴点P的坐标是(﹣2,2),
∵所求直线l与x﹣2y﹣1=0垂直,
∴可设直线l的方程为2x+y+C=0.
把点P的坐标代入得2×(﹣2)+2+C=0,即C=2.
∴所求直线l的方程为2x+y+2=0.
(2)解:又直线l的方程2x+y+2=0在x轴、y轴上的截距分别是﹣1与﹣2.
则直线l关于原点对称的直线在x轴、y轴上的截距分别是1与2,
∴所求直线方程为2x+y﹣2=0
【解析】(1)联立方程,求出点P的坐标,利用所求直线l与x﹣2y﹣1=0垂直,可设直线l的方程为2x+y+C=0,代入P的坐标,可求直线l的方程;(2)求出直线l的方程2x+y+2=0在x轴、y轴上的截距,可得直线l关于原点对称的直线在x轴、y轴上的截距,从而可求直线l关于原点O对称的直线方程.
【考点精析】掌握一般式方程是解答本题的根本,需要知道直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0).
(A,B不同时为0).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x﹣ ![]() )+
)+ ![]() .
.
(1)求函数f(x)的对称轴方程;
(2)若方程sin2x+2|f(x+ ![]() )|﹣m+1=0在x∈
)|﹣m+1=0在x∈ ![]() 上有三个实数解,求实数m的取值范围.
上有三个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校组织自主招生考试,其有2 000名学生报名参加了笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275).如图是按上述分组方法得到的频率分布直方图. 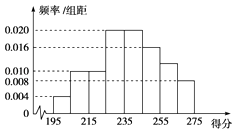
(1)从这2 000名学生中,任取1人,求这个人的分数在255~265之间的概率约是多少?
(2)求这2 000名学生的平均分数;
(3)若计划按成绩取1 000名学生进入面试环节,试估计应将分数线定为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣8≤0,x∈R},B={x|x2﹣(2m﹣3)x+m2﹣3m≤0,x∈R,m∈R }.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若ARB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只口袋内装有大小相同的5只球,其中3只白球2只黑球,从中一次摸出两只球.
(1)共有多少个基本事件,并列出.
(2)摸出的两只球都是白球的概率.
(3)摸出的两只球是一黑一白的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =3
=3 ![]() 1﹣2
1﹣2 ![]() 2 ,
2 , ![]() =4
=4 ![]() 1+
1+ ![]() 2 , 其中
2 , 其中 ![]() 1=(1,0),
1=(1,0), ![]() 2=(0,1),求:
2=(0,1),求:
(1)![]()
![]() 和|
和| ![]() +
+ ![]() |的值;
|的值;
(2)![]() 与
与 ![]() 夹角θ的余弦值.
夹角θ的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com