
【题目】某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的![]() )和两个半圆构成,设
)和两个半圆构成,设![]() ,且
,且![]() .
.

(1)若内圈周长为![]() ,则
,则![]() 取何值时,矩形
取何值时,矩形![]() 的面积最大?
的面积最大?
(2)若景观带的内圈所围成区域的面积为![]() ,则
,则![]() 取何值时,内圈周长最小?
取何值时,内圈周长最小?
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】近年来,随着“雾霾”天出现的越来越频繁,很多人为了自己的健康,外出时选择戴口罩,长郡中学高三兴趣研究小组利用暑假空闲期间做了一项对人们雾霾天外出时是否戴口罩的调查,共调查了120人,其中女性70人,男性50人,并根据统计数据画出等高条形图如图所示:
(Ⅰ)利用图形判断性别与雾霾天外出戴口罩是否有关系;
(Ⅱ)根据统计数据建立一个![]() 列联表;
列联表;
(Ⅲ)能否在犯错误的概率不超过0.05的前提下认为性别与雾霾天外出戴口罩有关系.
附: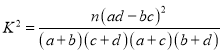

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是现代生活中进行信息交流的重要工具.据统计,某公司200名员工中![]() 的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中
的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中![]() 是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中
是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中![]() 都是青年人.
都是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,完成![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(2)由列联表中所得数据判断,能否在犯错误的概率不超过![]() 的前提下认为“经常使用微信与年龄有关”?
的前提下认为“经常使用微信与年龄有关”?
| 0.010 | 0.001 |
| 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆具有如下性质:若椭圆的方程为![]() ,则椭圆在其上一点
,则椭圆在其上一点![]() 处的切线方程为
处的切线方程为![]() ,试运用该性质解决以下问题:椭圆
,试运用该性质解决以下问题:椭圆![]() :
:![]() ,其焦距为2,且过点
,其焦距为2,且过点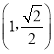 .点
.点![]() 为
为![]() 在第一象限中的任意一点,过
在第一象限中的任意一点,过![]() 作
作![]() 的切线
的切线![]() ,
,![]() 分别与
分别与![]() 轴和
轴和![]() 轴的正半轴交于
轴的正半轴交于![]() 两点,则
两点,则![]() 面积的最小值为( )
面积的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com