
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=![]() -1.其中
-1.其中![]() >0且
>0且![]() ≠1.
≠1.
(1)求f(2)+f(-2)的值;
(2)求f(x)的解析式;
(3)解关于x的不等式-1<f(x-1)<4.
【答案】(1)0;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由函数![]() 是奇函数,即可求得
是奇函数,即可求得![]() 的值;
的值;
(2)设![]() ,则
,则![]() ,求得
,求得![]() ,根据函数
,根据函数![]() 是奇函数,即可化简求得函数的解析式;
是奇函数,即可化简求得函数的解析式;
(3)分类讨论,得出不等式组,利用对数函数的性质,即可求解.
(1)∵f(x)是奇函数,
∴f(-2)=-f(2),即f(2)+f(-2)=0.
(2)当x<0时,-x>0,
∴f(-x)=a-x-1.
由f(x)是奇函数,有f(-x)=-f(x),
∵f(-x)=a-x-1,
∴f(x)=-a-x+1(x<0).
∴所求的解析式为f(x)=![]() .
.
(3)不等式等价于![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
当a>1时,有![]() 或
或![]() ,
,
注意此时loga2>0,loga5>0,可得此时不等式的解集为(1-loga2,1+loga5).
同理可得,当0<a<1时,不等式的解集为R.
综上所述,当a>1时,不等式的解集为(1-loga2,1+loga5);
当0<a<1时,不等式的解集为![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】(Ⅰ)![]() .
.
令![]() ,得
,得![]() .
.

![]() 与
与![]() 的情况如上:
的情况如上:
所以,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(Ⅱ)当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() ,即
,即![]() 时,
时,
由(Ⅰ)知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
综上,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
【题型】解答题
【结束】
19
【题目】已知抛物线![]() 的顶点在原点,焦点在坐标轴上,点
的顶点在原点,焦点在坐标轴上,点![]() 为抛物线
为抛物线![]() 上一点.
上一点.
(1)求![]() 的方程;
的方程;
(2)若点![]() 在
在![]() 上,过
上,过![]() 作
作![]() 的两弦
的两弦![]() 与
与![]() ,若
,若![]() ,求证: 直线
,求证: 直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 为正方形,四边形
为正方形,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若过直线![]() 的一个平面与线段
的一个平面与线段![]() 和
和![]() 分别相交于点
分别相交于点![]() 和
和![]() (点
(点![]() 与点
与点![]() 均不重合),求证:
均不重合),求证: ![]() ;
;
(3)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .点
.点![]() 为圆
为圆![]() 上任意一点,
上任意一点, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 相切,
相切, ![]() 与圆
与圆![]() 相交于另一点
相交于另一点![]() ,点
,点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,证明:直线
,证明:直线![]() 与椭圆
与椭圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.
(1)求抛物线C的方程;
(2)设直线y=kx+b与抛物线C交于A(x1 , y1),B(x2 , y2),且|y1﹣y2|=2,过弦AB中点M作平行于x轴的直线交抛物线于点D,求△ABD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(b﹣1)x+1(a,b∈R,a>0).
(1)若f(1)=0,且对任意x∈R,都有f(2﹣x)=f(2+x),求f(x)的解析式;
(2)已知x1 , x2为函数f(x)的两个零点,且x2﹣x1=2,当x∈(x1 , x2)时,g(x)=﹣f(x)+2(x2﹣x)的最大值为,当a≥2时,求h(a)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如下表:

若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”.已知“网购达人”与“网购探者”人数的比例为2:3.
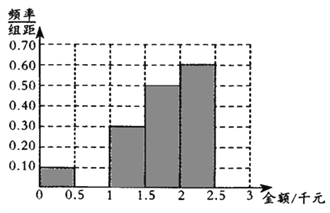
(1)确定![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日被评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com