
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线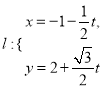 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 都是真命题,则命题“
都是真命题,则命题“![]() ”为真命题
”为真命题
B. 命题“![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. 命题:“若![]() ,则
,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() 或
或![]() ”
”
D. “![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是类比推理的( )
A. 两条直线平行,同旁内角互补,如果![]() 和
和![]() 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则![]()
B. 由平面三角形的性质,推测空间四边形的性质
C. 某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员.
D. 一切偶数都能被2整除,![]() 是偶数,所以
是偶数,所以![]() 能被2整除.
能被2整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过椭圆
经过椭圆![]() 的右顶点
的右顶点![]() 、下顶点
、下顶点![]() 和上顶点
和上顶点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)直线![]() 经过点
经过点![]() 且与
且与![]() 垂直,
垂直,![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的切线,切点分别为
的切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖励金额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:![]() ,
,![]() ,
,![]() ,其中哪个模型能符合公司的要求?
,其中哪个模型能符合公司的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列函数的奇偶性:
(1)f(x)=x+1;
(2)f(x)=x3+3x,x∈[-4,4);
(3)f(x)=|x-2|-|x+2|;
(4)f(x)=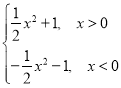
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数![]() ,单位是
,单位是![]() ,其中x表示鲑鱼的耗氧量的单位数.
,其中x表示鲑鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是8100个单位时,它的游速是多少?
(2)计算一条鲑鱼静止时耗氧量的单位数.
(3)若鲑鱼A的游速大于鲑鱼B的游速,问这两条鲑鱼谁的耗氧量较大?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数:

经计算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数, ![]() .
.
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (结果精确到
(结果精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,且相关指数为
,且相关指数为![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好;
说明哪种模型的拟合效果更好;
(ii)用拟合效果好的模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
, ![]() ,……,
,……, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:  ;相关指数为:
;相关指数为:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
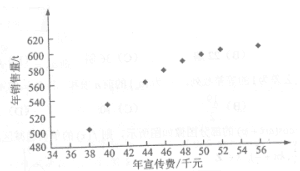
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() =
=![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利z与x,y的关系为![]() ,根据(Ⅱ)的结果回答下列问题:
,根据(Ⅱ)的结果回答下列问题:
(Ⅰ)当年宣传费![]() 时,年销售量及年利润的预报值时多少?
时,年销售量及年利润的预报值时多少?
(Ⅱ)当年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
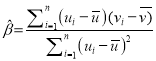 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com