
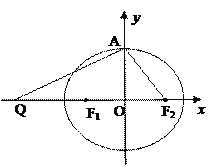
【题目】如图,设椭圆![]() 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且![]() 0,若过 A,Q,F2三点的圆恰好与直线
0,若过 A,Q,F2三点的圆恰好与直线![]() 相切,过定点 M(0,2)的直线
相切,过定点 M(0,2)的直线![]() 与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线
与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线![]() 的斜率
的斜率![]() ,在x轴上是否存在点P(
,在x轴上是否存在点P(![]() ,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出
,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,请说明理由;(Ⅲ)若实数
的取值范围;如果不存在,请说明理由;(Ⅲ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)利用向量确定F1为F2Q中点,设Q的坐标为(-3c,0),因为AQ⊥AF2,所以b2=3c×c=3c2,a2=4c×c=4c2,再由直线与圆相切得![]() 解得c=1,利用椭圆基本量之间的关系求b;(2)假设存在,设
解得c=1,利用椭圆基本量之间的关系求b;(2)假设存在,设![]() 方程,联立方程组,消元后由判别式大于0可得出
方程,联立方程组,消元后由判别式大于0可得出![]() ,又四边形为菱形时,对角线互相垂直,利用向量处理比较简单,
,又四边形为菱形时,对角线互相垂直,利用向量处理比较简单,![]() ,化简得(x1+x2)-2m+k2(x1+x2)+4k=0,再由
,化简得(x1+x2)-2m+k2(x1+x2)+4k=0,再由![]() 代入化简得:
代入化简得: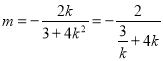 ,
,
解得![]() ,利用均值不等式范围;(3) 斜率存在时设直线方程,联立消元,
,利用均值不等式范围;(3) 斜率存在时设直线方程,联立消元,![]() ,再由
,再由![]() ,进行坐标运算,代入化简
,进行坐标运算,代入化简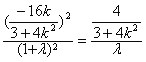 ,分离k与
,分离k与![]() ,利用k的范围求
,利用k的范围求![]() ,注意验证斜率不存在时情况.
,注意验证斜率不存在时情况.
试题解析:(1)因为![]() 0,所以F1为F2Q中点
0,所以F1为F2Q中点
设Q的坐标为(-3c,0),因为AQ⊥AF2,所以b2=3c×c=3c2,a2=4c×c=4c2,
且过A,Q,F2三点的圆的圆心为F1(-c,0),半径为2c.
因为该圆与直线L相切,所以![]() 解得c=1,所以a=2,
解得c=1,所以a=2,![]() 故所求椭圆方程为
故所求椭圆方程为![]() .(2)设L1的方程为y=kx+2(k>0)由
.(2)设L1的方程为y=kx+2(k>0)由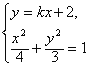 得(3+4k2)x2+16kx+4=0,
得(3+4k2)x2+16kx+4=0,
由△>0,得![]() 所以k>1/2,设G(x1,y1),H(x2,y2),则
所以k>1/2,设G(x1,y1),H(x2,y2),则![]() 所以
所以![]() (x1-m,y1)+(x2-m,y2)=(x1+x2-2m,y1+y2)=(x1+x2-2m,k(x1+x2)+4)
(x1-m,y1)+(x2-m,y2)=(x1+x2-2m,y1+y2)=(x1+x2-2m,k(x1+x2)+4)![]() (x2-x1,y2-y1)=(x2-x1,k(x2-x1)),由于菱形对角线互相垂直,因此
(x2-x1,y2-y1)=(x2-x1,k(x2-x1)),由于菱形对角线互相垂直,因此![]() 所以(x2-x1)[(x1+x2)-2m]+k(x2-x1)[k(x1+x2)+4]=0,故(x2-x1)[(x1+x2)-2m+k2(x1+x2)+4k]=0因为k>0,所以x2-x1≠0所以(x1+x2)-2m+k2(x1+x2)+4k=0,即(1+k2)(x1+x2)+4k-2m=0,所以
所以(x2-x1)[(x1+x2)-2m]+k(x2-x1)[k(x1+x2)+4]=0,故(x2-x1)[(x1+x2)-2m+k2(x1+x2)+4k]=0因为k>0,所以x2-x1≠0所以(x1+x2)-2m+k2(x1+x2)+4k=0,即(1+k2)(x1+x2)+4k-2m=0,所以
![]() ,解得
,解得![]() , 因为k>0,所以
, 因为k>0,所以![]() 故存在满足题意的点P且m的取值范围是
故存在满足题意的点P且m的取值范围是![]() .(3)①当直线L1斜率存在时,设直线L1方程为y=kx+2,代入椭圆方程
.(3)①当直线L1斜率存在时,设直线L1方程为y=kx+2,代入椭圆方程![]() ,得(3+4k2)x2+16kx+4=0 , 由△>0,得
,得(3+4k2)x2+16kx+4=0 , 由△>0,得![]() ,设G(x1,y1),H(x2,y2), 则
,设G(x1,y1),H(x2,y2), 则![]() ,又
,又![]() ,所以(x1,y1-2)=λ(x2,y2-2), 所以x1=λx2, 所以
,所以(x1,y1-2)=λ(x2,y2-2), 所以x1=λx2, 所以 ,∴
,∴![]() ∴
∴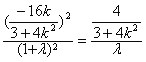 ,整理得
,整理得 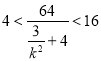 ,因为
,因为![]() , 所以
, 所以![]()
![]() ,解得
,解得![]() 又0<λ<1,所以
又0<λ<1,所以![]() .②当直线L1斜率不存在时,直线L1的方程为x=0,
.②当直线L1斜率不存在时,直线L1的方程为x=0,
![]() span>
span> ![]() ,
,![]() ,
,![]() ,所以
,所以![]() .综上所述,
.综上所述,![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂生产一批零件,为了解这批零件的质量状况,检验员从这批产品中随机抽取了100件作为样本进行检测,将它们的重量(单位:g)作为质量指标值.由检测结果得到如下频率分布直方图.
分组 | 频数 | 频率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合计 | 100 | 1 |
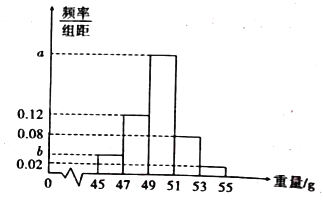
(1)求图中![]() 的值;
的值;
(2)根据质量标准规定:零件重量小于47或大于53为不合格品,重量在区间![]() 和
和![]() 内为合格品,重量在区间
内为合格品,重量在区间![]() 内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该零件重量的概率分布.若这批零件共
内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该零件重量的概率分布.若这批零件共![]() 件
件![]() ,现有两种销售方案:方案一:不再检测其他零件,整批零件除对已检测到的不合格品进行回收处理,其余零件均按150元/件售出;方案二:继续对剩余零件的重量进行逐一检测,回收处理所有不合格品,合格品按150元/件售出,优质品按200元/件售出.仅从获得利润大的角度考虑,该生产商应选择哪种方案?请说明理由.
,现有两种销售方案:方案一:不再检测其他零件,整批零件除对已检测到的不合格品进行回收处理,其余零件均按150元/件售出;方案二:继续对剩余零件的重量进行逐一检测,回收处理所有不合格品,合格品按150元/件售出,优质品按200元/件售出.仅从获得利润大的角度考虑,该生产商应选择哪种方案?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如题所示:扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条三条商业街道PQ、QR、RP,要求街道PQ与AB垂直,街道PR与AC垂直,直线PQ表示第三条街道。
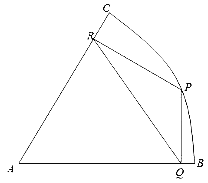
(1)如果P位于弧BC的中点,求三条街道的总长度;
(2)由于环境的原因,三条街道PQ、PR、QR每年能产生的经济效益分别为每千米300万元、200万元及400万元,问:这三条街道每年能产生的经济总效益最高为多少?(精确到1万元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳
月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳![]() 的质量
的质量![]() 随时间
随时间![]() (单位:年)的衰变规律满足
(单位:年)的衰变规律满足![]() (
(![]() 表示碳
表示碳![]() 原有的质量),则经过
原有的质量),则经过![]() 年后,碳
年后,碳![]() 的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳
的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳![]() 的质量是原来的
的质量是原来的![]() 至
至![]() ,据此推测良渚古城存在的时期距今约在________年到
,据此推测良渚古城存在的时期距今约在________年到![]() 年之间.(参考数据:
年之间.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
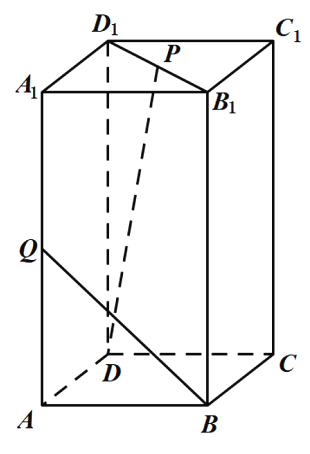
(1)试在线段![]() 上确定点
上确定点![]() 的位置,使得异面直线
的位置,使得异面直线![]() 与
与![]() 所成角为
所成角为![]() ,并请说明你的理由;
,并请说明你的理由;
(2)在满足(1)的条件下,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的点(点
上的点(点![]() 与
与![]() 、
、![]() 不重合),则下列结论正确的个数为( )
不重合),则下列结论正确的个数为( )
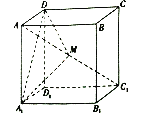
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③若![]() 的面积为
的面积为![]() ,则
,则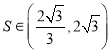 ;
;
④若![]() 、
、![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() ,
,![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() ,
,![]() 重合于点
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
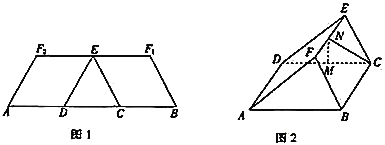
(1)证明:![]() 平面
平面![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() (
(![]() ),直线
),直线![]() :
:![]() ,
,![]() 与
与![]() 交于P、Q两点,
交于P、Q两点,![]() 为P关于y轴的对称点,直线
为P关于y轴的对称点,直线![]() 与y轴交于点
与y轴交于点![]() ;
;
(1)若点![]() 是
是![]() 的一个焦点,求
的一个焦点,求![]() 的渐近线方程;
的渐近线方程;
(2)若![]() ,点P的坐标为
,点P的坐标为![]() ,且
,且![]() ,求k的值;
,求k的值;
(3)若![]() ,求n关于b的表达式.
,求n关于b的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com