
【题目】已知函数f(x)=sin(2x+ ![]() )﹣cos2x.
)﹣cos2x.
(1)求f(x)的最小正周期及x∈[ ![]() ,
, ![]() ]时f(x)的值域;
]时f(x)的值域;
(2)在△ABC中,角A、B、C所对的边为a,b,c,且角C为锐角,S△ABC= ![]() ,c=2,f(C+
,c=2,f(C+ ![]() )=
)= ![]() ﹣
﹣ ![]() .求a,b的值.
.求a,b的值.
【答案】
(1)解:f(x)=sin(2x+ ![]() )﹣cos2x=
)﹣cos2x= ![]() sin2x+
sin2x+ ![]() cos2x﹣
cos2x﹣ ![]() (2cos2x﹣1)﹣
(2cos2x﹣1)﹣ ![]() ,
,
= ![]() sin2x﹣
sin2x﹣ ![]() ,
,
f(x)的最小正周期π,
x∈[ ![]() ,
, ![]() ],2x∈[
],2x∈[ ![]() ,
, ![]() ],
],
f(x)的值域[﹣ ![]() ,
, ![]() ﹣
﹣ ![]() ]
]
(2)解:f(x)= ![]() sin2x﹣
sin2x﹣ ![]() ,
,
f(C+ ![]() )=
)= ![]() sin2(C+
sin2(C+ ![]() )﹣
)﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴sin(2C+ ![]() )=
)= ![]() ,cos2C=
,cos2C= ![]() ,角C为锐角,
,角C为锐角,
C= ![]() ,
,
S= ![]() ,S△ABC=
,S△ABC= ![]() ,
,
ab=4 ![]() ,
,
由余弦定理可知:c2=a2+b2﹣2abcosC,
a2+b2=16,
解得b=2,a=2 ![]() 或b=2
或b=2 ![]() ,a=2
,a=2
【解析】(1)角和的正弦公式及二倍角公式,化简求得f(x)═ ![]() sin2x﹣
sin2x﹣ ![]() ,根据正弦函数的图象和性质,求出周期和f(x)的值域;
,根据正弦函数的图象和性质,求出周期和f(x)的值域;
(2)f(C+ ![]() )=
)= ![]() ﹣
﹣ ![]() ,求得C=
,求得C= ![]() ,由三角形的面积公式求得ab=4
,由三角形的面积公式求得ab=4 ![]() ,余弦定理求得a2+b2=16,联立求得a、b的值.
,余弦定理求得a2+b2=16,联立求得a、b的值.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,函数f(x)=2cosxsin(x﹣A)+sinA(x∈R)在x= ![]() 处取得最大值.
处取得最大值.
(1)当 ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,则( )
)的部分图象如图所示,则( )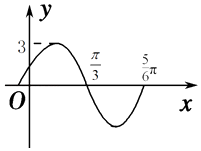
A.f(x)的一个对称中心为 ![]()
B.f(x)的图象关于直线 ![]() 对称
对称
C.f(x)在 ![]() 上是增函数
上是增函数
D.f(x)的周期为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省高考改革新方案,不分文理科,高考成绩实行“3+3”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体S,从学生群体S中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如表:
选考物理、化学、生物的科目数 | 1 | 2 | 3 |
人数 | 5 | 25 | 20 |
(I)从所调查的50名学生中任选2名,求他们选考物理、化学、生物科目数量不相等的概率;
(II)从所调查的50名学生中任选2名,记X表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量X的分布列和数学期望;
(III)将频率视为概率,现从学生群体S中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作Y,求事件“y≥2”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(2+x)=f(x),且在[﹣3,﹣2]上是减函数,若A、B是锐角三角形ABC的两个内角,则下列各式一定成立的是( )
A.f(sinA)<f(cosB)
B.f(sinA)>f(cosB)
C.f(sinA)>f(sinB)
D.f(cosA)>f(cosB)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com