
【题目】如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.

求证:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.
【答案】(1)详见解析;(2)详见解析.
【解析】
试题分析:(1) 由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC,根据线面平行的判定定理得证;(2)由CC1⊥平面ABC,可得AC⊥CC1,又因为AC⊥BC,由线面垂直的判定定理可得AC⊥平面BCC1B1,进而可得B1C⊥AC,又BC1⊥B1C,证得BC1⊥平面B1AC,故命题成立.
试题解析:
(1)由题意知,E为B1C的中点,
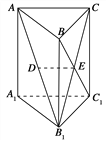
又D为AB1的中点,因此DE∥AC.
又因为DE平面AA1C1C,AC平面AA1C1C,
所以DE∥平面AA1C1C.
(2)因为棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC.
因为AC平面ABC,所以AC⊥CC1.
又因为AC⊥BC,CC1平面BCC1B1,
BC平面BCC1B1,BC∩CC1=C,
所以AC⊥平面BCC1B1,
又因为BC1平面BCC1B1,所以B1C⊥AC.
因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.
因为AC,B1C平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.
又因为AB1平面B1AC,所以BC1⊥AB1.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,左焦点为
,左焦点为![]() ,右焦点为
,右焦点为![]() ,短轴两个端点
,短轴两个端点![]() 、
、![]() ,与
,与![]() 轴不垂直的直线
轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,记直线
,记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)求证直线![]() 与
与![]() 轴相交于定点,并求出定点坐标;
轴相交于定点,并求出定点坐标;
(3)当弦![]() 的中点
的中点![]() 落在
落在![]() 内(包括边界)时,求直线
内(包括边界)时,求直线![]() 的斜率的取值.
的斜率的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.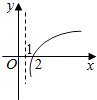
B.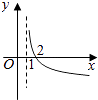
C.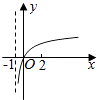
D.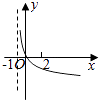
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 ![]() (α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程
(2)若直线l的极坐标方程为ρ(sinθ+cosθ)=1,求直线l被曲线C截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 圆心为
圆心为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .
.
(![]() )求
)求![]() 的取值范围;
的取值范围;
(![]() )是否存在常数
)是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奥地利遗传学家孟德尔1856年用豌豆作实验时,他选择了两种性状不同的豌豆,一种是子叶颜色为黄色,种子性状为圆形,茎的高度为长茎,另一种是子叶颜色为绿色,种子性状为皱皮,茎的高度为短茎。我们把纯黄色的豌豆种子的两个特征记作![]() ,把纯绿色的豌豆的种子的两个特征记作
,把纯绿色的豌豆的种子的两个特征记作![]() ,实验杂交第一代收获的豌豆记作
,实验杂交第一代收获的豌豆记作![]() ,第二代收获的豌豆出现了三种特征分别为
,第二代收获的豌豆出现了三种特征分别为![]() ,
,![]() ,
,![]() ,请问,孟德尔豌豆实验第二代收获的有特征
,请问,孟德尔豌豆实验第二代收获的有特征![]() 的豌豆数量占总收成的( )
的豌豆数量占总收成的( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在框图中,设x=2,并在输入框中输入n=4;ai=i(i=0,1,2,3,4).则此程序执行后输出的S值为( )

A. 26 B. 49 C. 52 D. 98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在坐标原点,焦点在坐标轴上,且经过
中心在坐标原点,焦点在坐标轴上,且经过![]() 三点.
三点.
(1)求椭圆![]() 的方程;
的方程;
(2)在直线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,分别与椭圆
,分别与椭圆![]() 交于
交于![]() 两点,判断直线
两点,判断直线![]() 是否过定点?若是,求出该定点.若不是,请说明理由.
是否过定点?若是,求出该定点.若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com