
| A. | y=ex | B. | y=lnx | C. | y=x2 | D. | y=$\frac{x-1}{x+1}$ |
分析 由自变量与对应的函数值不相等判断A,B,D不合题意;举例说明C正确.
解答 解:函数y=ex在定义域内为增函数,而ex>x恒成立,∴不存在实数m使得定义域和值域都是(m,+∞);
函数y=lnx在定义域内为增函数,而x>lnx恒成立,∴不存在实数m使得定义域和值域都是(m,+∞);
当m=0时,y=x2的定义域和值域都是(m,+∞),符合题意;
对于$y=\frac{x-1}{x+1}$,由$\frac{x-1}{x+1}=x$,得x2=-1,方程无解,∴不存在实数m使得定义域和值域都是(m,+∞).
故选:C.
点评 本题考查函数的定义域及其求法,考查了函数的值域,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 有且仅有一条 | B. | 有且仅有两条 | C. | 有无穷多条 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,lnx0<0 | B. | ?x∈(-∞,0),ex>0 | ||
| C. | ?x>0,5x>3x | D. | ?x0∈(0,+∞),2<sinx0+cosx0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
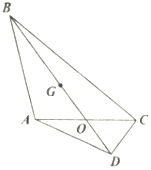 如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.
如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | $1+\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com