
【题目】已知正方体的棱长为2,平面![]() 过正方体的一个顶点,且与正方体每条棱所在直线所成的角相等,则该正方体在平面
过正方体的一个顶点,且与正方体每条棱所在直线所成的角相等,则该正方体在平面![]() 内的正投影面积是__________.
内的正投影面积是__________.
科目:高中数学 来源: 题型:
【题目】在直角坐标系中![]() 中,曲线C的参数方程
中,曲线C的参数方程![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线
).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设P是曲线C上的一个动点,当![]() 时,求点P到直线
时,求点P到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线C上所有的点均在直线![]() 的右下方,求t的取值范围.
的右下方,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M为BC的中点,将△AMB沿直线AM翻折成△AB1M,连接B1D,N为B1D的中点,则在翻折过程中,下列说法正确的是( )
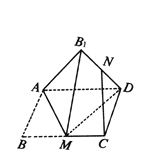
A.存在某个位置,使得CN⊥AB1
B.CN的长是定值
C.若AB=BM,则AM⊥B1D
D.若AB=BM=1,当三棱锥B1-AMD的体积最大时,三棱锥B1-AMD的外接球的表面积是4π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名物理学家李政道说:“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的,它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例,把八度分成13个半音,使相邻两个半音之间的频率比是常数,如下表所示,其中![]() 表示这些半音的频率,它们满足
表示这些半音的频率,它们满足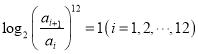 .若某一半音与
.若某一半音与![]() 的频率之比为
的频率之比为![]() ,则该半音为( )
,则该半音为( )
频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
半音 | C |
| D |
| E | F |
| G |
| A |
| B | C(八度) |
A.![]() B.GC.
B.GC.![]() D.A
D.A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一世”又叫“一代”.东汉·王充《论衡·宜汉篇》:“且孔子所谓一世,三十年也”,清代·段玉裁《说文解字注》:“三十年为一世,按父子相继曰世”.而当代中国学者测算“一代”平均为25年.另根据国际一家研究机构的研究报告显示,全球家族企业的平均寿命其实只有26年,约占总量的![]() 的家族企业只能传到第二代,约占总量的
的家族企业只能传到第二代,约占总量的![]() 的家族企业只能传到第三代,约占总量
的家族企业只能传到第三代,约占总量![]() 的家族企业可以传到第四代甚至更久远(为了研究方便,超过四代的可忽略不计).根据该研究机构的研究报告,可以估计该机构所认为的“一代”大约为( )
的家族企业可以传到第四代甚至更久远(为了研究方便,超过四代的可忽略不计).根据该研究机构的研究报告,可以估计该机构所认为的“一代”大约为( )
A.23年B.22年C.21年D.20年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为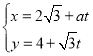 (其中t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点A的极坐标为
(其中t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点A的极坐标为![]() ,直线
,直线![]() 经过点A.曲线C的极坐标方程为
经过点A.曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线C于D,E两点(D在x轴上方),求
的垂线交曲线C于D,E两点(D在x轴上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,其图象如图所示.函数
,其图象如图所示.函数![]() 是定义域为
是定义域为![]() 的奇函数,满足
的奇函数,满足![]() ,且当
,且当![]() 时,
时,![]() .给出下列三个结论:
.给出下列三个结论:
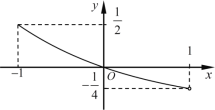
①![]() ;
;
②函数![]() 在
在![]() 内有且仅有
内有且仅有![]() 个零点;
个零点;
③不等式![]() 的解集为
的解集为![]() .
.
其中,正确结论的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com