
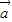 •
•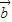 =
=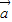 •
•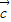 ,则
,则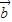 =
=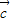
 ”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件.
”是“一元二次方程x2+x+m=0”有实数解的充分不必要条件. 时,显然不成立;利用函数的单调性定义,易判断③的对错;利用二次方程的解的情况取决于判别式,令判别式大于等于0求出m的范围即后面的条件;判断前者成立是否能推出后者成立;反之后者成立能否推出前者,易判断④的对错;⑤函数零点左右两边函数值的符号相反,根据函数在一个区间上两个端点的函数值的符号确定是否存在零点.故⑤正确
时,显然不成立;利用函数的单调性定义,易判断③的对错;利用二次方程的解的情况取决于判别式,令判别式大于等于0求出m的范围即后面的条件;判断前者成立是否能推出后者成立;反之后者成立能否推出前者,易判断④的对错;⑤函数零点左右两边函数值的符号相反,根据函数在一个区间上两个端点的函数值的符号确定是否存在零点.故⑤正确 时,显然不成立;第一象限的角是无数个不连续的区间构成,由函数单调性的定义,易得③错误;,∵一元二次方程x2+x+m=0,m∈R有实数解∴△=1-4m≥0,解得m
时,显然不成立;第一象限的角是无数个不连续的区间构成,由函数单调性的定义,易得③错误;,∵一元二次方程x2+x+m=0,m∈R有实数解∴△=1-4m≥0,解得m ,若m
,若m  成立能推出 m
成立能推出 m  成立;反之当 m
成立;反之当 m  成立推不出 m<
成立推不出 m< 故④正确;⑤由
故④正确;⑤由 及零点定理知f(x)的零点在区间(-1,0)上,∴零点所在的一个区间是(a-1,a)是(-1,0)
及零点定理知f(x)的零点在区间(-1,0)上,∴零点所在的一个区间是(a-1,a)是(-1,0)

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+1 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
变量x与变量y,w,z的对应关系如下表所示:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com