
【题目】已知定义在![]() 上的函数
上的函数![]() .
.
(1)求![]() 单调区间;
单调区间;
(2)当![]() 时,
时,![]() 在
在![]() 上有三个零点,求
上有三个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
![]() 对函数
对函数![]() 求导可得,
求导可得,![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况讨论利用导数
三种情况讨论利用导数![]() 判断函数
判断函数![]() 的单调性求单调区间即可;
的单调性求单调区间即可;
![]() 令
令![]() ,把函数
,把函数![]() 在
在![]() 上有三个零点转化为函数
上有三个零点转化为函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有三个不同的交点,通过对函数
上有三个不同的交点,通过对函数![]() 进行求导判断其单调性并求极值,得到关于
进行求导判断其单调性并求极值,得到关于![]() 的不等式,解不等式即可.
的不等式,解不等式即可.
![]() 由题意知,
由题意知,![]() ,
,
令![]() 得
得![]() 或
或![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时由
时由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ;
;
![]() 函数
函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
当![]() 时由
时由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ;
;
![]() 函数
函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
综上可知,当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时函数
时函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
当![]() 时函数
时函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
![]() 令
令![]() ,则
,则![]() ,
,
则![]() ,令
,令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 或
或![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 有极大值为
有极大值为![]() ,
,
当![]() 时,函数
时,函数![]() 有极小值为
有极小值为![]() ,
,
使函数![]() 在
在![]() 上有三个零点,
上有三个零点,
即直线![]() 和函数
和函数![]() 有三个不同的交点,
有三个不同的交点,
由![]() 单调性,只需满足
单调性,只需满足![]() ,
,
即![]() ,解得
,解得![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄 (单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=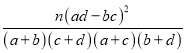 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在给出的下列命题中,正确的是( )
A.设![]() 是同一平面上的四个点,若
是同一平面上的四个点,若![]() ,则点
,则点![]() 必共线
必共线
B.若向量![]() 是平面
是平面![]() 上的两个向量,则平面
上的两个向量,则平面![]() 上的任一向量
上的任一向量![]() 都可以表示为
都可以表示为![]() ,且表示方法是唯一的
,且表示方法是唯一的
C.已知平面向量![]() 满足
满足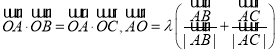 则
则![]() 为等腰三角形
为等腰三角形
D.已知平面向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 是等边三角形
是等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下列结论正确的个数有( )
,则下列结论正确的个数有( )
①![]() 是函数
是函数![]() 图像的一条对称轴
图像的一条对称轴
②![]() 是函数
是函数![]() 图像的一个对称中心
图像的一个对称中心
③将函数![]() 图像向右平移
图像向右平移![]() 单位所得图像的解析式为得
单位所得图像的解析式为得![]()
④函数![]() 在区间
在区间![]() 内单调递增
内单调递增
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
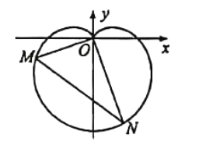
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (m为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(m为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 与曲线C交于M,N两点.
与曲线C交于M,N两点.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com