
【题目】已知函数![]()
(Ⅰ)若函数![]() 在其定义域上为单调函数,求
在其定义域上为单调函数,求![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 的图像在
的图像在![]() 处的切线的斜率为0,
处的切线的斜率为0,![]() ,已知
,已知![]() 求证:
求证:![]()
(Ⅲ)在(2)的条件下,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)略;(Ⅲ)
;(Ⅱ)略;(Ⅲ)![]() <
<![]() .
.
【解析】
试题(Ⅰ)利用导数求解单调性,把恒成立转化为最值;(Ⅱ)可用数学归纳法来证明![]() ;(Ⅲ)通过放缩法来解决
;(Ⅲ)通过放缩法来解决![]() 与
与![]() 的大小比较问题.
的大小比较问题.
试题解析:(Ⅰ) ∵f(1)="a-b=0" ∴a=b
∴![]()
∴![]()
要使函数![]() 在其定义域上为单调函数,则在定义域(0,+∞)内
在其定义域上为单调函数,则在定义域(0,+∞)内![]() 恒大于等于0或恒小于等于0,
恒大于等于0或恒小于等于0,
当a=0时,![]() 在(0,+∞)内恒成立;
在(0,+∞)内恒成立;
当a>0时,![]() 恒成立,则
恒成立,则![]() ∴
∴![]()
当a<0时,![]() 恒成立
恒成立
∴a的取值范围是:![]()
(Ⅱ)![]() ∴a=1 则:
∴a=1 则:![]()
于是![]()
用数学归纳法证明![]() 如下:
如下:
当n=1时,![]() ,不等式成立;
,不等式成立;
假设当n=k时,不等式![]() 成立,即
成立,即![]() 也成立,
也成立,
当n=k+1时,![]()
所以当n=k+1时不等式成立,
综上得对所有![]() 时,都有
时,都有![]()
(Ⅲ)由(2)得![]()
![]()
于是![]()
所以![]()
![]() ,
,![]()
累乘得:![]() 则
则![]()
所以![]()
![]()


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
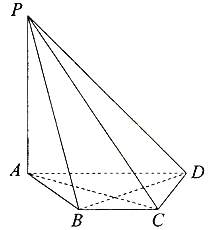
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产![]() 万件,需另投入流动成本
万件,需另投入流动成本![]() 万元,当年产量小于
万元,当年产量小于![]() 万件时,
万件时,![]() (万元);当年产量不小于7万件时,
(万元);当年产量不小于7万件时,![]() (万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(1)写出年利润![]() (万年)关于年产量
(万年)关于年产量![]() (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() .
.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从0,1,2,3,4这五个数中任选三个不同的数组成一个三位数,记X为所组成的三位数各位数字之和.
(1)求X是奇数的概率;
(2)求X的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
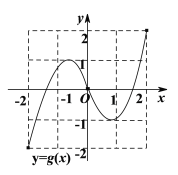
【题目】如图分别为定义域和值域均为![]() 的函数
的函数![]() 和函数
和函数![]() 的图象,则下列命题正确的是( )
的图象,则下列命题正确的是( )

A.函数![]() 恰有
恰有![]() 个零点B.函数
个零点B.函数![]() 恰有
恰有![]() 个零点
个零点
C.函数![]() 恰有
恰有![]() 个零点D.函数
个零点D.函数![]() 恰有
恰有![]() 个零点
个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com