
 设函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的两个相邻的对称中心分别为(${\frac{π}{8}$,0),(${\frac{5π}{8}$,0).
设函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的两个相邻的对称中心分别为(${\frac{π}{8}$,0),(${\frac{5π}{8}$,0).分析 (Ⅰ)由题意可求周期T,利用周期公式可求ω,由$f(\frac{π}{8})=sin({\frac{π}{4}+φ})=0$,结合范围-π<φ<0,可求φ,从而可求f(x)的解析式,由$2x-\frac{π}{4}=\frac{π}{2}+kπ,k∈Z$可解得f(x)对称轴方程.
(Ⅱ)分别求出对应的x值和y值列表,然后描点,再用平滑曲线连接得函数图象.
解答 解:(Ⅰ)∵f(x)的两个相邻的对称中心分别为$({\frac{π}{8},0})$,$({\frac{5π}{8},0})$,
∴${T}=\frac{4π}{8}×2=\frac{π}{2}×2=\frac{2π}{2}=π$,
∴ω=2,
∴f(x)=sin(2x+φ),
∵$f(\frac{π}{8})=sin({\frac{π}{4}+φ})=0$,
∴$\frac{π}{4}+φ=kπ,k∈Z$,
∴$φ=kπ-\frac{π}{4},k∈Z$,
∵-π<φ<0,
∴$φ=-\frac{π}{4}$,
∴$f(x)=sin({2x-\frac{π}{4}})$.…(4分)
由$2x-\frac{π}{4}=\frac{π}{2}+kπ,k∈Z$,得$x=\frac{3π}{8}+\frac{kπ}{2},k∈Z$,
所以f(x)对称轴方程为$x=\frac{3π}{8}+\frac{kπ}{2},k∈Z$,…(6分)
(Ⅱ)列表:
| x | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | $\frac{9π}{8}$ |
| $2x-\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| f(x) | 0 | 1 | 0 | -1 | 0 |
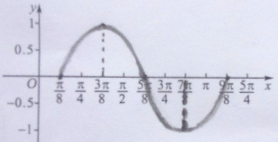
点评 本题考查了y=Asin(ωx+φ)型函数的有关概念,考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查利用五点作图法作函数的图象,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $[-1,\sqrt{2}]$ | B. | $[-\sqrt{2},\sqrt{2}]$ | C. | $[\sqrt{2}-2,2]$ | D. | $[1-\sqrt{2},1+\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{x^'}^2}}{4}+\frac{{{y^'}^2}}{3}=1$ | B. | $\frac{{{y^'}^2}}{4}+\frac{{{x^'}^2}}{3}=1$ | C. | x'2+y'2=1 | D. | x'2+y'2=12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 210种 | B. | 630种 | C. | 420种 | D. | 840种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
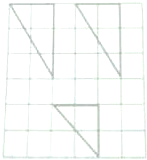 如图,网格纸上小正方体的边长为1,粗实线画出的是某多面体的三视图(第一个为主视图,下面的是俯视图),则该多面体各个面的面积最大值为$3\sqrt{2}$.
如图,网格纸上小正方体的边长为1,粗实线画出的是某多面体的三视图(第一个为主视图,下面的是俯视图),则该多面体各个面的面积最大值为$3\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com