
| A. | 48里 | B. | 24里 | C. | 12里 | D. | 6里 |
分析 由题意可知,每天走的路程里数构成以$\frac{1}{2}$为公比的等比数列,由S6=378求得首项,再由等比数列的通项公式求得该人第五天走的路程.
解答 解:记每天走的路程里数为{an},
由题意知{an}是公比$\frac{1}{2}$的等比数列,
由S6=378,得${S}_{6}=\frac{{a}_{1}(1-\frac{1}{{2}^{6}})}{1-\frac{1}{2}}$=378,
解得:a1=192,
∴${a}_{5}=192×\frac{1}{{2}^{4}}$=12(里).
故选:C.
点评 本题考查等比数列的通项公式的运用,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
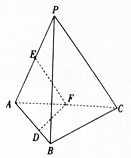 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [0,+∞) | C. | (4,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4] | B. | [3,4] | C. | (-∞,0)∪(0,4] | D. | (-∞,-1)∪(0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$单位即可 | B. | 向右平移$\frac{π}{6}$单位即可 | ||
| C. | 向右平移$\frac{π}{3}$单位即可 | D. | 向左平移$\frac{π}{3}$单位即可 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com