Question

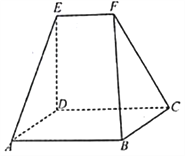
【题目】如图，多面体ABCDEF中，四边形ABCD是矩形，EF∥AD，FA⊥面ABCD，AB=AF=EF=1，AD=2，AC交BD于点P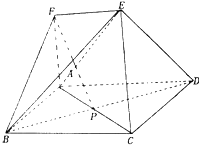

（1）证明：PF∥面ECD；
（2）求二面角B﹣EC﹣A的大小．

Answer 1

【答案】
（1）证明：取CD中点G，连结EG、PG，

∵点P为矩形ABCD对角线交点，

∴在△ACD中，PG AD，

又EF=1，AD=2，EF∥AD，∴EF PG，

∴四边形EFPG是平行四边形，

∴FP∥EG，

又FP平面ECD，EG平面ECD，

∴FP∥平面ECD．

（2）解：由题意，以AB所在直线为x轴，

AD所在直线为y轴，AF所在直线为z轴，建立空间直角坐标系，

则F（0，0，1），B（1，0，0），C（1，2，0），E（0，1，1），

∴ =（0，2，0）， =（1，1，﹣1）， =（1，2，0），

取FB中点H，连结AH，则 =（ ），

∵ =0， =0，

∴AH⊥平面EBC，

故取平面AEC法向量为 =（ ），

设平面AEC的法向量 =（x，y，1），

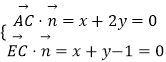则 ，∴ =（2，﹣1，1），

cos＜ ＞= = = ，

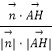∴二面角B﹣EC﹣A的大小为 ．

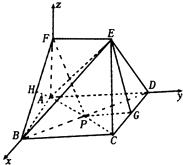
【解析】（1）取CD中点G，连结EG、PG，推导出四边形EFPG是平行四边形，由此能证明FP∥平面ECD．（2）以AB所在直线为x轴，AD所在直线为y轴，AF所在直线为z轴，建立空间直角坐标系，利用向量法能求出二面角B﹣EC﹣A的大小．
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案，需要熟知平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．