
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知bcosC=(2a﹣c)cosB. (Ⅰ)求B;
(Ⅱ)若c=2,b=3,求△ABC的面积.
【答案】解:(Ⅰ)由已知及正弦定理得sinBcosC=(2sinA﹣sinC)cosB=2sinAcosB﹣sinCcosB. 则sinBcosC+sinCcosB=2sinAcosB.
sin(B+C)=2sinAcosB,
故sinA=2sinAcosB.
因为,在△ABC中,sinA≠0.
所以 ![]() ,
, ![]() .
.
(Ⅱ)由已知及余弦定理得9=4+a2﹣4acosB,
又 ![]() ,
,
所以:a2﹣2a﹣5=0,解得:a=1+ ![]() ,或a=1﹣
,或a=1﹣ ![]() (舍去),
(舍去),
所以:S△ABC= ![]() acsinB=
acsinB= ![]() (1+
(1+ ![]() )×
)× ![]() =
= ![]()
【解析】(Ⅰ)由已知及正弦定理,两角和的正弦函数公式,三角形内角和定理,诱导公式化简可得sinA=2sinAcosB.结合sinA≠0.可求cosB,利用特殊角的三角函数值即可求得B的值.(Ⅱ)由已知及余弦定理得a2﹣2a﹣5=0,解得a的值,进而利用三角形面积公式即可得解.
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,已知点P(2,0),且正方形ABCD内接于⊙O:x2+y2=1,M、N分别为边AB、BC的中点.当正方形ABCD绕圆心O旋转时, ![]() 的取值范围为 .
的取值范围为 . 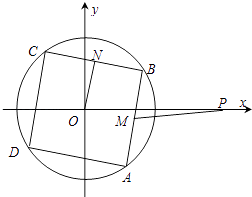
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[不等式选讲]
设函数f(x)=a(x﹣1).
(Ⅰ)当a=1时,解不等式|f(x)|+|f(﹣x)|≥3x;
(Ⅱ)设|a|≤1,当|x|≤1时,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月某校高三年级1600名学生参加了教育局组织的期末统考,已知数学考试成绩X~N(100,σ2)(试卷满分为150分).统计结果显示数学考试成绩在80分到120分之间的人数约为总人数的 ![]() ,则此次统考中成绩不低于120分的学生人数约为( )
,则此次统考中成绩不低于120分的学生人数约为( )
A.80
B.100
C.120
D.200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的短轴长为2
的短轴长为2 ![]() ,离心率e=
,离心率e= ![]() ,
,
(1)求椭圆C的标准方程:
(2)若F1、F2分别是椭圆C的左、右焦点,过F2的直线l与椭圆C交于不同的两点A、B,求△F1AB的内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy 中,直线l的参数方程为 ![]() ,(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点o为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ. (Ⅰ)求圆C在直角坐标系中的方程;
,(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点o为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ. (Ⅰ)求圆C在直角坐标系中的方程;
(Ⅱ)若圆C与直线l相切,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年下半年,锦阳市教体局举行了市教育系统直属单位职工篮球比赛,以增强直属单位间的交流与合作,组织方统计了来自A1 , A2 , A3 , A4 , A5等5个直属单位的男子篮球队的平均身高与本次比赛的平均得分,如表所示:
单位 | A1 | A2 | A3 | A4 | A5 |
平均身高x(单位:cm) | 170 | 174 | 176 | 181 | 179 |
平均得分y | 62 | 64 | 66 | 70 | 68 |
注:回归当初 ![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为  ,
, ![]() .
.
(1)根据表中数据,求y关于x的线性回归方程;(系数精确到0.01)
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设M,N为两个随机事件,给出以下命题: (1.)若M、N为互斥事件,且 ![]() ,
, ![]() ,则
,则 ![]() ;
;
(2.)若 ![]() ,
, ![]() ,
, ![]() ,则M、N为相互独立事件;
,则M、N为相互独立事件;
(3.)若 ![]() ,
, ![]() ,
, ![]() ,则M、N为相互独立事件;
,则M、N为相互独立事件;
(4.)若 ![]() ,
, ![]() ,
, ![]() ,则M、N为相互独立事件;
,则M、N为相互独立事件;
(5.)若 ![]() ,
, ![]() ,
, ![]() ,则M、N为相互独立事件;
,则M、N为相互独立事件;
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在常数k(k∈N* , k≥2)、q、d,使得无穷数列{an}满足  则称数列{an}为“段比差数列”,其中常数k、q、d分别叫做段长、段比、段差.设数列{bn}为“段比差数列”.
则称数列{an}为“段比差数列”,其中常数k、q、d分别叫做段长、段比、段差.设数列{bn}为“段比差数列”.
(1)若{bn}的首项、段长、段比、段差分别为1、3、q、3. ①当q=0时,求b2016;
②当q=1时,设{bn}的前3n项和为S3n , 若不等式 ![]() 对n∈N*恒成立,求实数λ的取值范围;
对n∈N*恒成立,求实数λ的取值范围;
(2)设{bn}为等比数列,且首项为b,试写出所有满足条件的{bn},并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com