
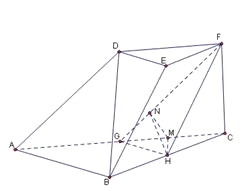
【题目】如图,在三棱台![]() 中,
中,![]() 分别为
分别为![]() 的中点.
的中点.
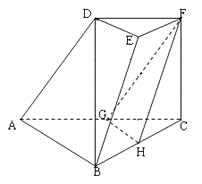
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,
,![]() ,
,
![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角(锐角)的大小.
所成角(锐角)的大小.
【答案】(Ⅰ)略;(Ⅱ)![]()
【解析】
试题(Ⅰ)思路一:连接![]() ,设
,设![]() ,连接
,连接![]() ,先证明
,先证明![]() ,从而由直线与平面平行的判定定理得
,从而由直线与平面平行的判定定理得![]() 平面
平面![]() ;思路二:先证明平面
;思路二:先证明平面![]() 平面
平面![]() ,再由平面与平面平行的定义得到
,再由平面与平面平行的定义得到![]() 平面
平面![]() .
.
(Ⅱ)思路一:连接![]() ,设
,设![]() ,连接
,连接![]() ,证明
,证明![]() 两两垂直, 以
两两垂直, 以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,利用空量向量的夹角公式求解;思路二:作
,利用空量向量的夹角公式求解;思路二:作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,连接
,连接![]() ,证明
,证明![]() 即为所求的角,然后在三角形中求解.
即为所求的角,然后在三角形中求解.
试题解析:
(Ⅰ)证法一:连接![]() ,设
,设![]() ,连接
,连接![]() ,
,
在三棱台![]() 中,
中,
![]() 为
为![]() 的中点
的中点
可得![]()
所以四边形![]() 为平行四边形
为平行四边形
则![]() 为
为![]() 的中点
的中点
又![]() 为
为![]() 的中点
的中点
所以![]()
又![]() 平面
平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
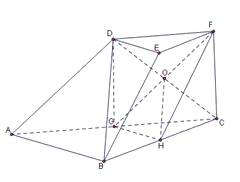
证法二:
在三棱台![]() 中,
中,
由![]() 为
为![]() 的中点
的中点
可得![]()
所以四边形![]() 为平行四边形
为平行四边形
可得![]()
在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
所以![]()
又![]() ,所以平面
,所以平面![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以![]() 平面
平面![]()
(Ⅱ)解法一:
设![]() ,则
,则![]()
在三棱台![]() 中,
中,
![]() 为
为![]() 的中点
的中点
由![]() ,
,
可得四边形![]() 为平行四边形,
为平行四边形,
因此![]()
又![]() 平面
平面![]()
所以![]() 平面
平面![]()
在![]() 中,由
中,由![]() ,
,![]() 是
是![]() 中点,
中点,
所以![]()
因此![]() 两两垂直,
两两垂直,
以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]()
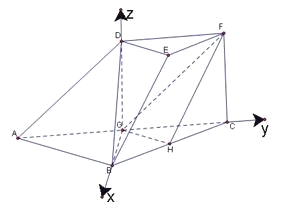
所以![]()
可得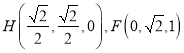
故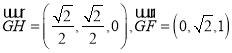
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
由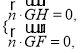 可得
可得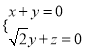
可得平面![]() 的一个法向量
的一个法向量![]()
因为![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]()
所以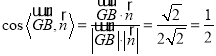
所以平面与平面所成的解(锐角)的大小为![]()
解法二:
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,连接
,连接![]()
由![]() 平面
平面![]() ,得
,得![]()
又![]()
所以![]() 平面
平面![]()
因此![]()
所以![]() 即为所求的角
即为所求的角
在![]() 中,
中,![]()
由![]() ∽
∽![]()
可得![]()
从而![]()
由![]() 平面
平面![]() 平面
平面![]()
得![]()
因此![]()
所以![]()
所以平面![]() 与平面
与平面![]() 所成角(锐角)的大小为
所成角(锐角)的大小为![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】一间宿舍内住有甲乙两人,为了保持宿舍内的干净整洁,他们每天通过小游戏的方式选出一人值日打扫卫生,游戏规则如下:第1天由甲值日,随后每天由前一天值日的人抛掷两枚正方体骰子(点数为![]() ),若得到两枚骰子的点数之和小于10,则前一天值日的人继续值日,否则当天换另一人值日.从第2天开始,设“当天值日的人与前一天相同”为事件
),若得到两枚骰子的点数之和小于10,则前一天值日的人继续值日,否则当天换另一人值日.从第2天开始,设“当天值日的人与前一天相同”为事件![]() .
.
(1)求![]() .
.
(2)设![]() 表示“第
表示“第![]() 天甲值日”的概率,则
天甲值日”的概率,则![]() ,其中
,其中![]() ,
,![]() .
.
(ⅰ)求![]() 关于
关于![]() 的表达式.
的表达式.
(ⅱ)这种游戏规则公平吗?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 | 总计 |
男 | 10 | 8 | 7 | 3 | 2 | 15 | 45 |
女 | 5 | 4 | 6 | 4 | 6 | 30 | 55 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 | 100 |
(1)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,能否在犯错误概率不超过0.005的前提下,认为是否为“移动支付活跃用户”与性别有关?
(2)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户.
①求抽取的4名用户中,既有男“移动支付达人”又有女“移动支付达人”的概率;
②为了鼓励男性用户使用移动支付,对抽出的男“移动支付达人”每人奖励300元,记奖励总金额为X,求X的分布列及均值.
附公式及表如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)某县一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨、硝酸盐15吨.先库存磷酸盐10吨、硝酸盐66吨,在此基础上生产这两种混合肥料.若生产1车皮甲种肥料产生的利润为10000元;生产1车皮乙种肥料产生的利润为5000元.那么分别生产甲、乙两种肥料各多少车皮能产生最大的利润?
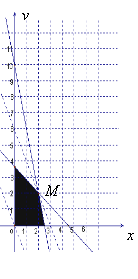
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com